Dans les pages sur les droites du modèle de Hilbert, on a vu que, du point de vue de la géométrie dynamique, c’est-à-dire pour la construction effective d’une droite définie par deux points, il faut distinguer trois types de droites, selon la position des points par rapport à l’ellipse de référence du modèle de Hilbert. On a alors appelé
• Cas 1 : les deux points sont extérieurs à l’ellipse.
• Cas 2 : les deux points sont intérieurs à l’ellipse.
• Cas 3 : un des points est à l’intérieur, l’autre à l’extérieur.
On a vu que, comme il a été traité ici, pour le moment, le cas 3 est assez lourd à mettre en œuvre, nécessitant une bonne pratique du logiciel. Aussi les macros proposées dans cet article ne concernent que les deux premiers cas, purement géométriques, pour lesquels on a déjà développé des figures assez consistantes, avec, parfois, des résultats significatifs,que l’on peut parcourir à nouveau rapidement ici pour le cas 1 et là pour le cas 2.
Dans une première partie, on présente les macros mises à disposition, leurs usages, et dans une seconde partie, des propositions d’utilisations assez simples (Rappels pour la pratique des macros).
Les macros de modèle de Hilbert non arguésien

On dispose donc de 5 macros seulement, ce qui signifie que, en particulier dans le cas 1, une bonne partie des figures se fait avec l’usage classique du logiciel, usage rapidement présenté dans la seconde partie de cette page. Nous y reviendrons aussi en détail.
H droite F Ell A B
Cette macro-construction trace la H-droite \((AB)\) dans le cas où \(A\) et \(B\) sont tous les deux soit intérieurs à l’ellipse soit extérieurs à l’ellipse. On montre simplement, dans l’ordre le point \(F\), l’ellipse, les points \(A\) et \(B\). La macro construit la droite en laissant apparents les points d’intersection avec l’ellipse, ainsi que le centre de l’arc de cercle euclidien associé. Ces points sont différents dans les deux cas, avec le suffixe \(ee\) ou \(ii\) selon le cas.
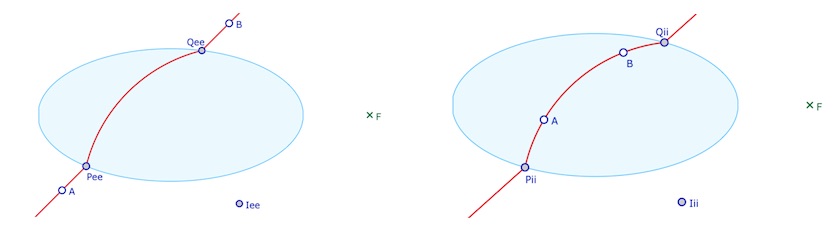
Lancer la figure de base dans un nouvel onglet.
La figure contient déjà trois points nommés.
Cette macro générale, sera plus particulièrement utile dans le cas des points intérieurs à l’ellipse car, souvent, pour poursuivre la construction, on aura besoin du centre de l’arc de cercle. Pour le cas des points extérieurs, on utilisera plutôt la macro suivante …
H droite nette F Ell A B
La même que la précédente, sans les trois points \(P_{ee}, Q_{ee}, I_{ee}\).
Les trois dernières macros, elles, sont destinées au cas où les deux points constituants de la droites sont à l’intérieur de l’ellipse, et donc en pratique, s’appliquent, par exemple, à des triangles intérieurs à
l’ellipse.
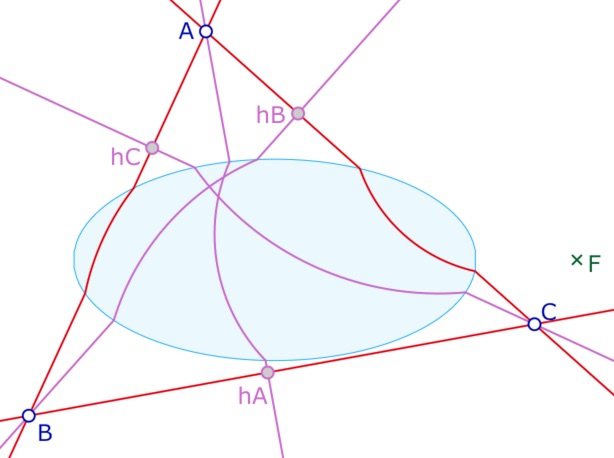
hB par F cAC C B
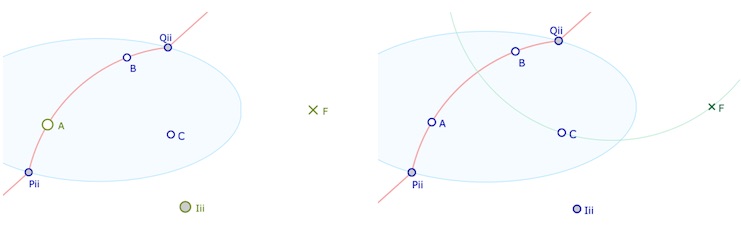
Cette macro, dans la dénomination de son nom, construit le cercle passant par \(B\) – et \(F\) pour être une H-droite – orthogonal à l’arc passant par \(A\) et \(C\) pour être une droite orthogonale. On montre le point \(F\), puis centre \(cAB\) de l’arc de cercle, le point \(C\), et en dernier le point \(B\) d’où est issue la perpendiculaire.
Pour construire, comme ci-dessous, la perpendiculaire à la droite \((AB)\) passant par le point \(C\), on commence par montrer (illustration de gauche), le point \(C\), le centre du cercle \(I_{ii}\) (pour \(cAB\)), puis le point \(A\). Il reste un point à montrer, le point d’où on veut la hauteur, donc le point \(C\) (illustration de droite), ce qui construit aussitôt le cercle solution.
inter Arc Cercle
Sert à construire le point d’intersection pied de la perpendiculaire de la seconde illustration. La nécessité d’une telle macro, en général pour les arcs de cercle, a été présentée ici.
S’applique aussi à l’intersection de deux arcs ou de deux cercles (en montrant l’intersection que l’on souhaite quand il y en a deux).
Milieu Arc AB cAB
Construit simplement le milieu de l’arc entre \(A\) et \(B\) en donnant le centre du cercle (\(I_{ii}\) dans les illustrations précédentes). Le point n’est pas nommé. Il apparaît comme une croix verte.
Applications successives de la macro-construction des H-droites
Les points d’intersections avec l’ellipse et le centre du cercle étant générés automatiquement, ils prennent le nom générique de la première application auquel est ajouté un suffixe numérique incrémenté à partir de 0.
Lancer la figure de base dans un nouvel onglet
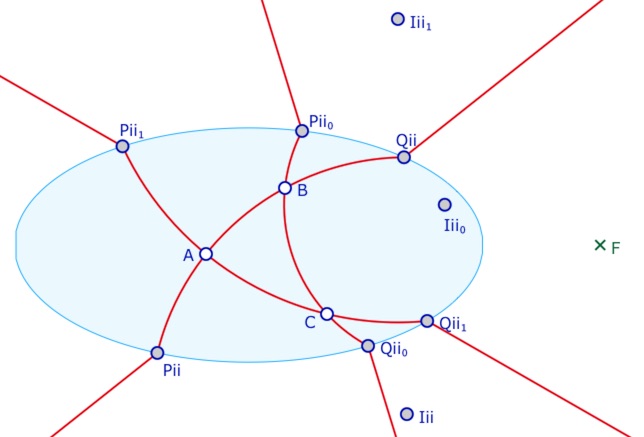
Ainsi dans l’illustration ci-contre, on voit que l’on a commencé par appliquer la macro aux points \(A\) et \(B\) (par les points \(P_{ii}, Q_{ii}\) et \(I_{ii}\) non suffixés), puis on a ensuite créé la droite \((BC)\) car on repère le suffixe 0 à ses points de contact avec l’ellipse \(P_{ii_0}, \, Q_{ii_0}\) ainsi que le nom du centre de l’arc \(I_{ii_0}\).
Enfin on a construit la droite \((AC)\) car on repère le suffixe suivant dans les points d’intersection \(P_{ii_1}, \, Q_{ii_1}\) ainsi que le centre \(I_{ii_1}\).
Dans l’illustration suivante, on a ensuite ajouté le H-milieu de \(A\) et \(B\). C’est le point vert, que l’on a ensuite nommé \(mAB\) avec l’inspecteur d’objet.
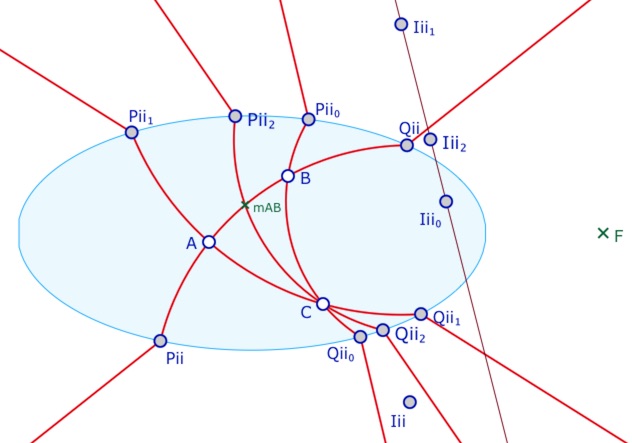
Puis on a construit la H-médiane du triangle avec la même macro H-droite.
On repère ses intersections \(P_{ii_2}, \, Q_{ii_2}\)et son centre \(I_{ii_2}\).
Ce dernier point est aligné avec \(I_{ii_0}\) et \(I_{ii_1}\) car ils sont tous les trois sur la médiatrice de \(C\) et \(F\). On peut ainsi explorer le concours des médianes et des hauteurs.
On remarquera que, sauf à vouloir nommer des points, toutes ses figures peuvent se faire uniquement en mode macro, ce qui ne sera pas le cas avec les points de base extérieurs à l’ellipse.
Utilisations simples de la macro H-droite dans le cas des points extérieurs à l’ellipse
L’utilisation devient un peu plus technique, car il faut aussi utiliser l’interface « constructive » du logiciel pour réaliser les constructions. On peut commencer par des utilisations minimales de cette interface.
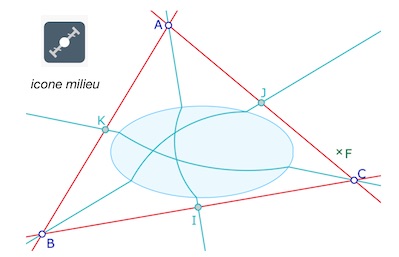
Médianes d’un triangle dont les sommets et les milieux sont tous extérieurs à l’ellipse.
La figure est très simple à réaliser : on utilise l’icone du milieu (de deux points ou d’un segment). Et on utilise la macro H-droite. Pour que le milieu euclidien soit le H-milieu il suffit que les côtés du triangle ne rencontrent pas l’ellipse.
Les parallélogrammes des milieux
Il suffit d’ajouter les droites \((IJ)\), \((JK)\), ou \((IK)\), \((JK)\), puisque les milieux sont extérieurs à la conique.
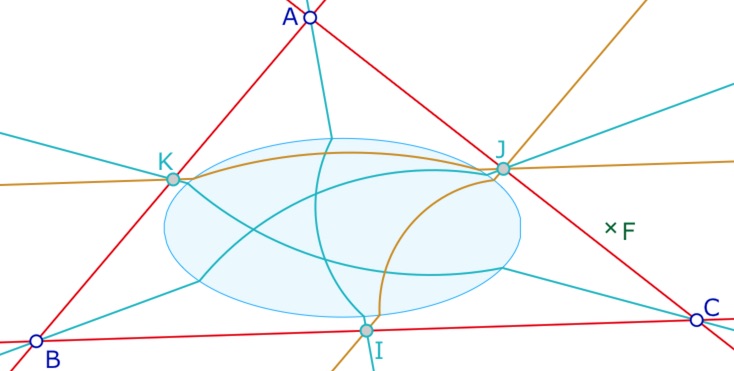
Hauteurs d’un triangle dont les pieds sont extérieurs à la conique.
Pour que l’on puisse faire cette figure avec les macros disponibles, il suffit que le pied de chaque hauteur soit extérieur à l’ellipse pour que l’orthogonalité euclidienne corresponde à celle du modèle de Hilbert. On note \(h_A, \, h_B, \, h_C\) les trois pieds des hauteurs construits simplement par les perpendiculaires euclidiennes. Il est préférable de cacher – avec l’outil gomme – les trois perpendiculaires avant d’appliquer la macro H-droite nette.
Réalisation de la configuration de Desargues
L’utilisation dans ce cas est plus technique, au sens il faut nettement plus manipuler le logiciel, et en particulier apprendre à utiliser les outils euclidiens pour réaliser cette construction. Dans cette section, on détaille comment réaliser la configuration de «Desargues affine» dans ce modèle, avec les 6 points \(A, B, C\) et \(A_1, B_1, C_1\), tous à l’extérieur de l’ellipse. Il est conseillé d’utiliser la seconde macro des H-droites, celle dite «nette», sinon la figure deviendrait lourde à lire.
Lancer la figure de base dans un nouvel onglet
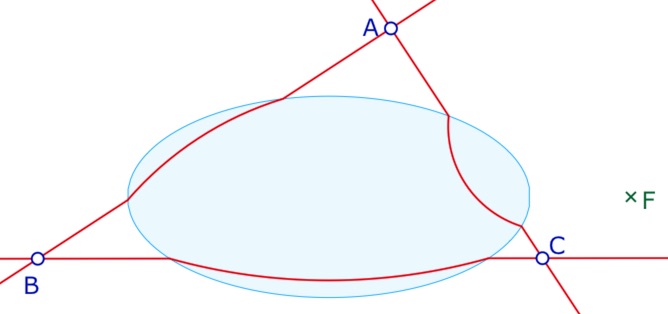
Commencer par construire les trois H-droites \((AB), \, (AC), \, (BC)\).
Ensuite construire un point \(A_1\) (que l’on peut ne pas nommer), un peu en dessous de \(A\), et en dehors de l’ellipse. Pour cela, passer en mode standard (flèche sélectionnée).
Construire une H-parallèle à une H-droite
On doit ensuite construire les H-parallèles aux H-droites \((AB)\) et \((AC)\) passant par un point \(A_1\). Les supports principaux de ces droites sont les parallèles aux droites euclidiennes \((AB)\) et \((AC)\). Pour poursuivre, il faut savoir comment sont construites les H-droites.
En effet, une H-droite \((AB)\) est constituée, soit de la droite euclidienne \((AB)\) si celle-ci ne coupe pas l’ellipse, soit de trois parties, deux demi-droites et un arc de cercle dans l’ellipse. En pratique on a les deux types qui apparaissent l’un ou l’autre selon les circonstances. Par construction, la droite euclidienne \((AB)\) existe toujours – elle est construite dans la macro – elle est juste cachée quand c’est l’autre type qui doit s’afficher. Par contre le second type n’existe que … s’il doit exister. Et donc ce second type n’existe pas si la H-droite \((AB)\) est la droite euclidienne.
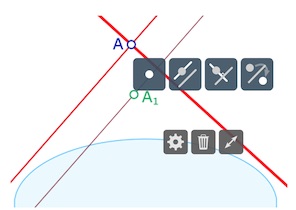
Il en résulte que, pour prendre une H-parallèle, il faut se placer dans le contexte où la H-droite est la droite euclidienne. En opérant ainsi, le support existera dans tous les cas. On pourra construire la H-droite à partir de ce support.
Ci-contre, on a déjà tracé, la parallèle à \((AB)\) et on s’apprête à construire celle parallèle à \((AC)\).
Rappels techniques : pour cela il faut être en mode standard. Pour prendre une parallèle, on montre d’abord la droite, cela ouvre la palette associée aux droites, puis on montre le point \(A_1\).
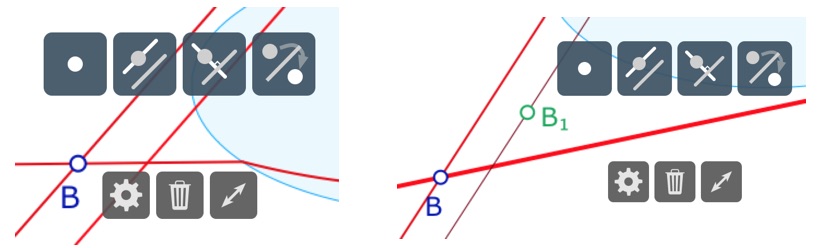
Puis on prend un point \(B_1\) sur la première parallèle euclidienne – icone « point » en sélectionnant la droite (ci-contre à gauche), puis on prend à nouveau une parallèle euclidienne (à droite) après avoir placé la H-droite \((BC)\) dans une instance où c’est la droite euclidienne.
Enfin on crée l’intersection des droites euclidiennes, ci-dessous à gauche, le point \(C_0\). Cette intersection ne peut pas s’appeler \(C_1\) car c’est un nom déjà utilisé par les macro précédentes. Puis, avec l’icone «gomme», on cache les trois droites euclidiennes.
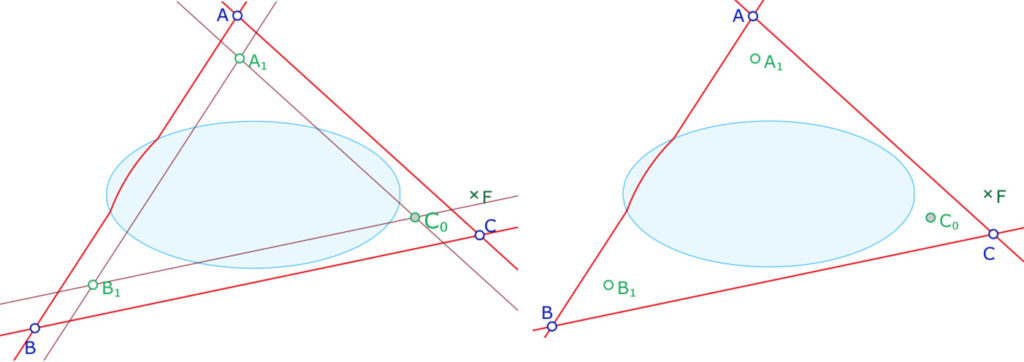
On utilise ensuite, à nouveau, la macro H-droite nette F Ell A B sur les points \(A_1, \, B_1\), puis \(A_1, \, C_0\) et \(B_1, \, C_0\). Si on les colorie, comme ci-dessous, penser à colorier aussi le cas où ce sont des droites euclidiennes. On termine la figure en appliquant à nouveau la macro H-droite sur les points \(A, \, A_1\), puis \(B, \, B_1\) et enfin \(C, \, C_1\) (coloriées en bleu dans l’illustration de droite). Dans la troisième illustration, on voit que si les intersections des droites [\((AA_1), \, (BB_1), (CC_1)\) sont en dehors de l’ellipse, ces points d’intersection sont confondus et la propriété de Desargues est vérifiée puisque c’est aussi le cas euclidien.
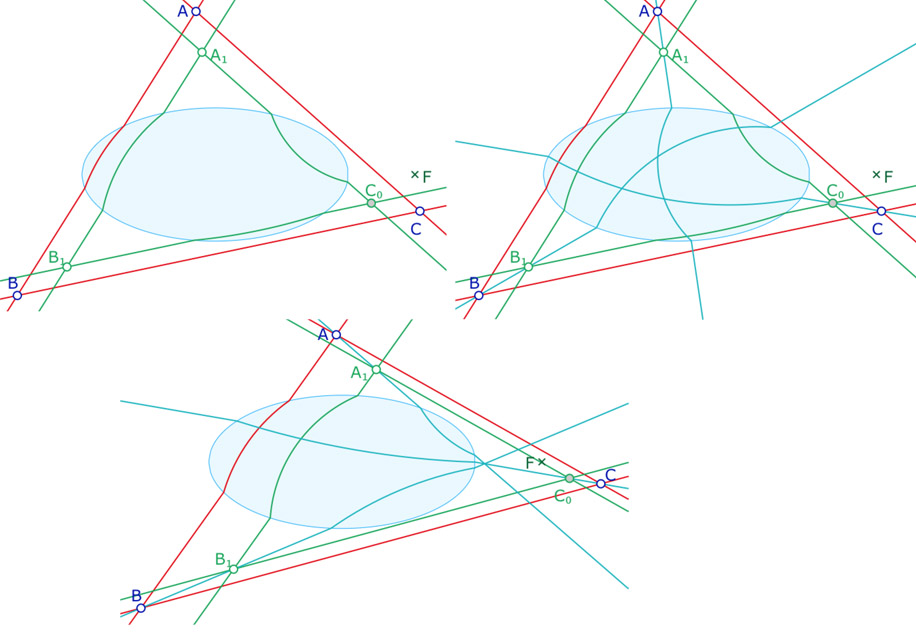
Réalisation de la configuration de Pappus
La figure est toute élémentaire à faire. On a choisi de la proposer pour aborder un autre point un peu plus technique, pour les personnes qui veulent aller plus loin dans la pratique du logiciel. Tout d’abord, il est préférable de ne pas utiliser les noms \(A’, \, B’, \, C’\) pour des points, c’est pour cela qu’on les note \(A_p, \, B_p, \, C_p\) dans la figure de départ que l’on peut charger.
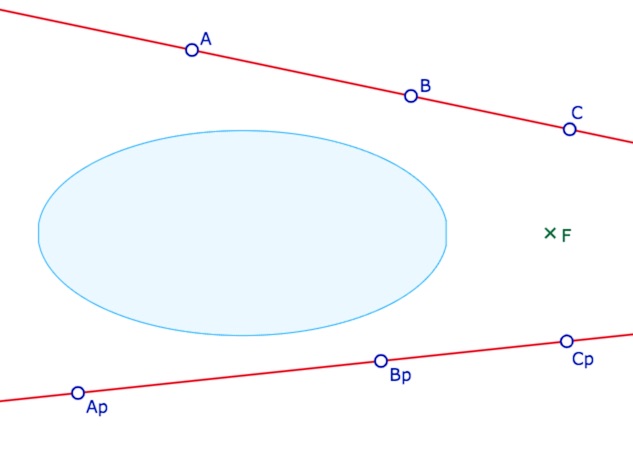
Lancer cette figure de départ dans un nouvel onglet (les droites sont bien des H-droites)
Commencer par réaliser cette figure, ie avec deux intersections à l’intérieur de l’ellipse et une à l’extérieur.
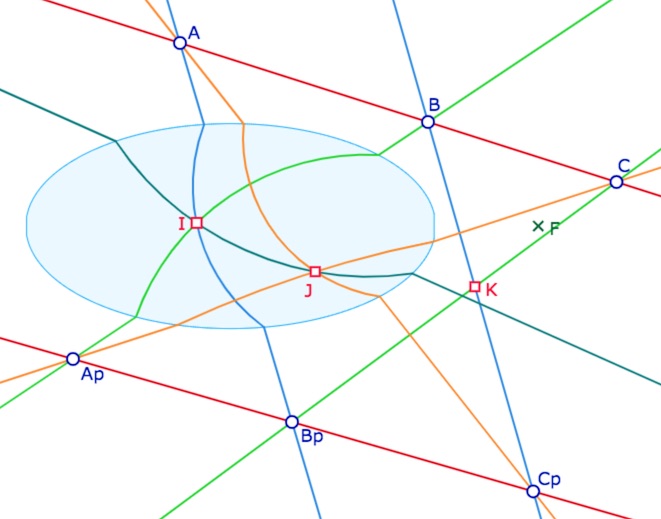
Les points d’intersection \(I, J, K\) ne sont pas alignés :
la configuration de Pappus n’est pas vraie en géométrie non arguésienne.
Le point \(K\) est construit d’abord comme intersection des deux H-droites quand elles sont toutes les deux des droites euclidiennes. Ce qui permet d’avoir naturellement cette configuration ou \(K\) est bien construit même si une des droites n’est pas euclidienne :
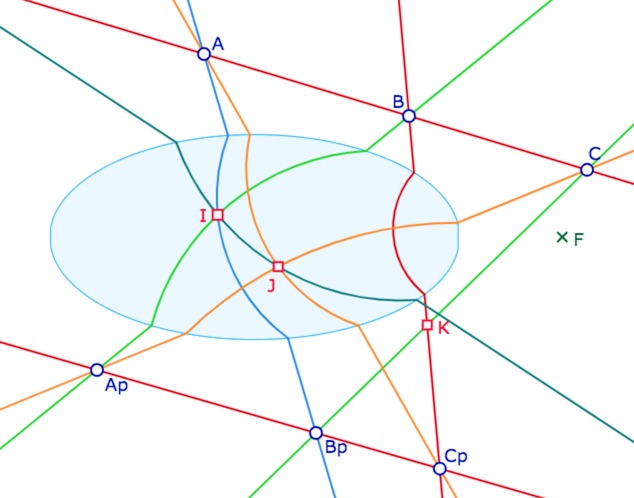
Complément technique
On commence par se placer dans cette situation où \(K\), à l’intérieur de l’ellipse, est renommé \(K_1\) et où on a construit \(K_2\) avec la macro inter Arc Cercle (sur les deux arcs bien entendu). On ajoute alors un nouveau point \(K\) qui va prendre la position de \(K_1\) ou \(K_2\) selon la situation.

Sur le point \(K\) sélectionné (on est donc en mode standard) on choisit l’icone « calculatrice », c’est-à-dire on se place en mode « expression » et on rentre l’expression suivante : si \(K_2\) n’existe pas, \(K\) va en \(K_1\) sinon il va en \(K_2\). Et \(K\) se place aussitôt au point qu’il convient.

Bien entendu, il faut ensuite cacher \(K_1\) et \(K_2\), et colorier les droites.
Si l’on n’a pas envie de rentrer dans ces manipulations, on peut préférer lancer la figure K-finalisée dans un nouvel onglet, et observer l’expression de \(K\) : mode standard, icone « calculatrice » sur le point \(K\).
La figure est seulement « K-finalisée » car il faudrait faire la même chose sur les points \(I\) et \(J\).