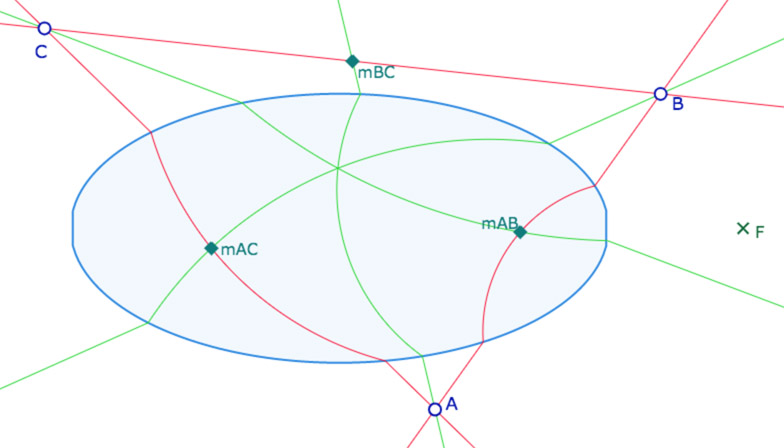
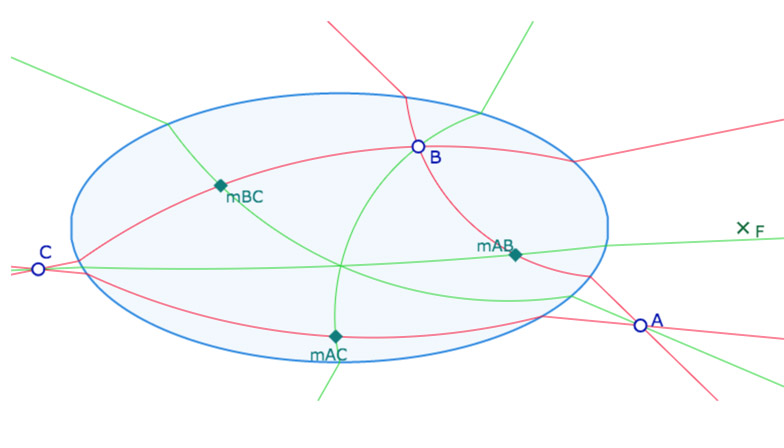
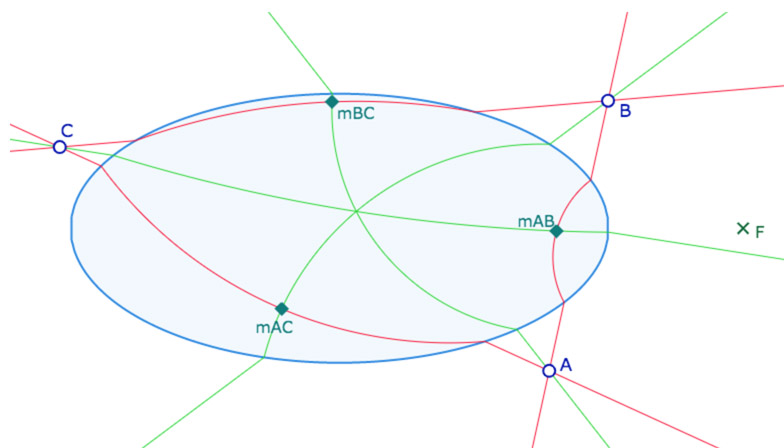
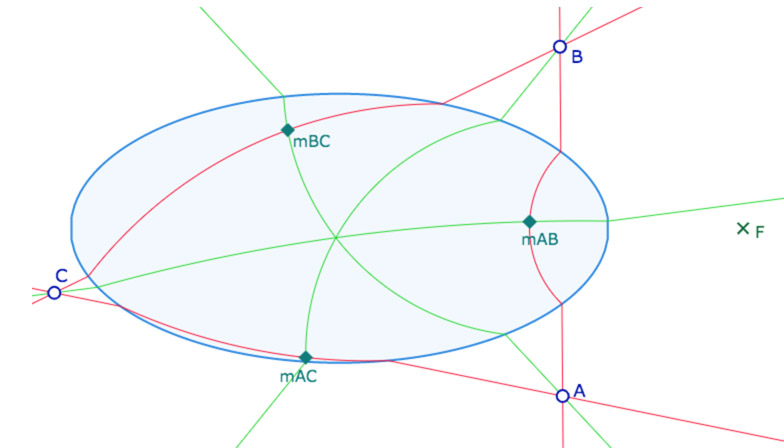
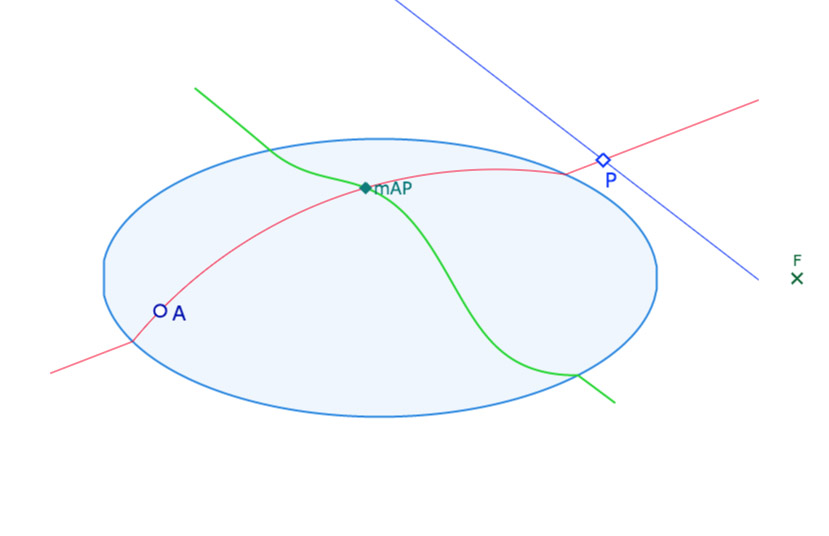
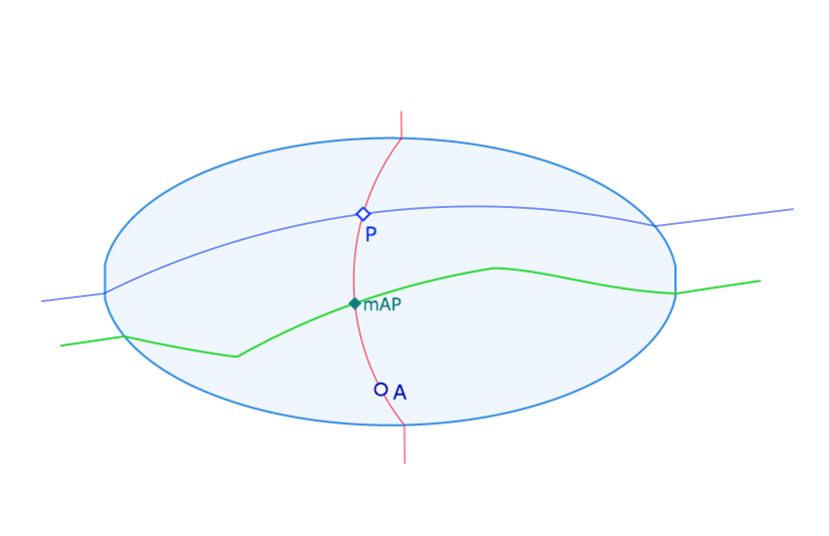
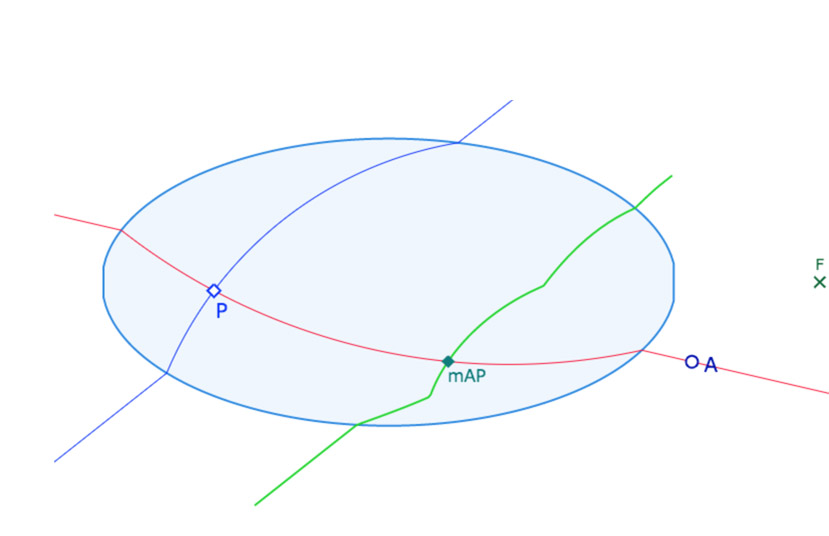
Hilbert considère le modèle de la géométrie euclidienne plane suivant. Il se donne l’ellipse centrée à l’origine du repère canonique, de grand axe 1 et de petit axe 1/2. Soit l’ellipse d’équation \(x^2+4y^2=1\). Puis il considère le point \(F \displaystyle \left( \frac{3}{2},0 \right)\) et montre que tout cercle passant par \(F\) et coupant l’ellipse, soit est tangent à l’ellipse, soit ne coupe l’ellipse qu’en deux points distincts. Plus précisément il montre que tout cercle coupant l’ellipse en 4 points ne passe pas par \(F\). Cela lui permet de définir une nouvelle géométrie de la façon suivante :
Droites et segments
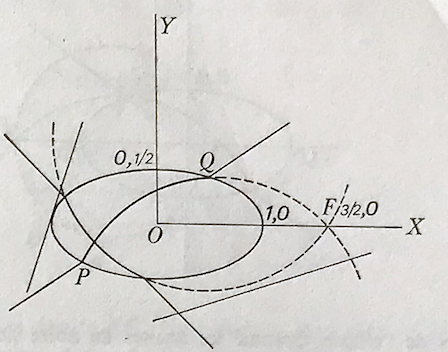
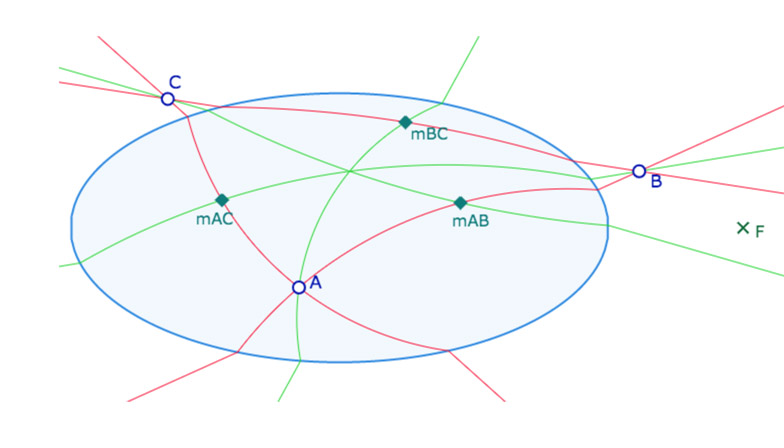
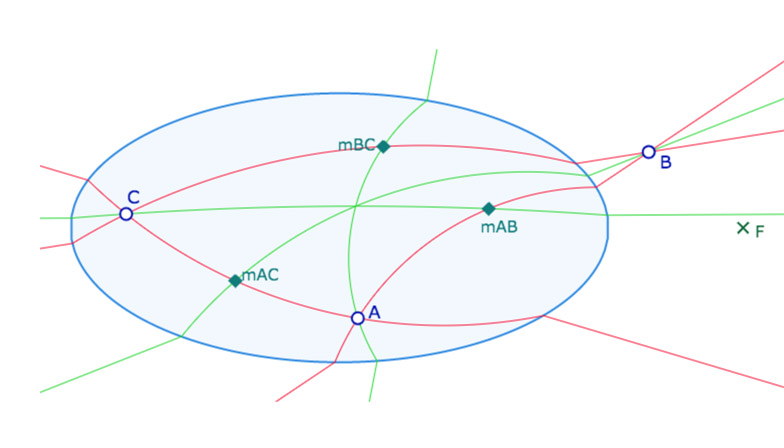
«Élaborons notre nouvelle géométrie comme suit. Comme points prenons les points du plan \(xy\). Comme droites, choisissons, sans modification, celles du plan qui ne coupent pas l’ellipse ou qui lui sont tangentes; par contre si une droite \(g\) coupe l’ellipse en deux points \(P\) et \(Q\), construisons le cercle passant par \(P\), \(Q\) et \(F\). Ce cercle ne coupe pas l’ellipse hors de ces points. Sur la droite \(g\) remplaçons le segment compris entre \(P\) et \(Q\) par l’arc du cercle précédent situé à l’intérieur de l’ellipse. Les deux demi-droites portées par \(g\) limitées à \(P\) et \(Q\) et l’arc de cercle ci-dessus constituent une droite de notre nouvelle géométrie(*). Supposons la construction effectuée pour toutes les droites du plan. Les droites de la nouvelle géométrie satisfont les axiomes (I.1 et I.2) et (IV). Les axiomes (II) sont aussi valables en considérant l’ordre naturel des points sur ces droites. Nous dirons que deux segments \(AB\) et \(A’B’\) sont congruents si les segments \(AB\) et \(A’B’\) mesurés éventuellement en tout ou partie sur un arc de cercle ont des longueurs habituelles égales. »
(*) Nous parlerons dans la suite de H-droite, pour droite de Hilbert, et de H-segment.
Angles
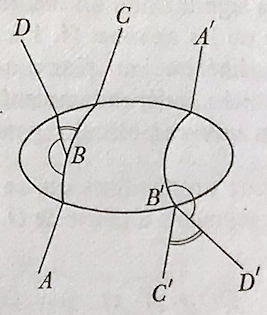
«Enfin il nous faut définir la congruence des angles. Si aucun des sommets des angles à comparer n’appartiennent à l’ellipse, nous dirons que les angles sont congruents s’ils le sont au sens ordinaire du terme. Dans le cas contraire, opérons comme suit :
Soient \(ABC\) et \(A’B’C’\) des points alignés ordonnés de notre géométrie, \(D\) un point extérieur à la droite \(ABC\) et \(D’\) hors de la droite \(A’B’C’\).
Nous dirons que les congruences suivantes d’angles sont satisfaites:
\(\angle ABD = \angle A’B’D’\) et \(\angle CBD = \angle C’B’D’\)
si les angles naturels correspondant sont liés par la proportion
\(\angle ABD : \angle CBD = \angle A’B’D’ : \angle C’B’D’\)
Grace à ces conventions les axiomes (III.1 à 4) sont valables.»
Entre les pages sur le modèle de Hilbert et celles sur le modèle de Moulton, nous proposons une « page interlude » analysant cette définition de la congruence des angles dont l’un a un sommet sur l’ellipse, en particulier car, comme l’a montré Moulton, elle ne vérifie pas vraiment l’axiome III.4 comme l’annonce un peu vite Hilbert.
Dans un premier temps, on retiendra que, pour les sommets hors de l’ellipse, les angles sont les angles euclidiens usuels.
La géométrie obtenue est non arguésienne
(exemple de Hilbert, statique)
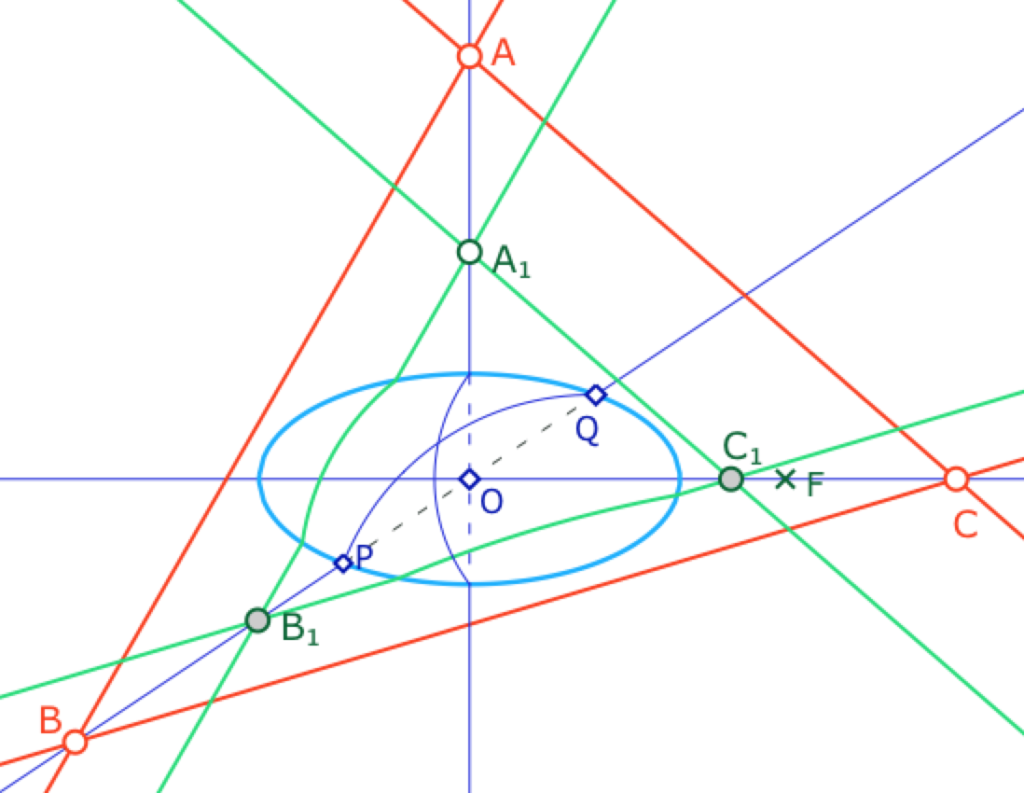
Pour illustrer que le théorème de Desargues n’est pas vérifié, Hilbert considère d’une part l’axe des abscisse – qui est une H-droite car cet axe est « le cercle » passant par F et les deux sommets de l’ellipse, puis la H-droite associée à l’axe des ordonnées et enfin celle passant par les points de l’ellipse \( \displaystyle \left( -\frac{3}{5},-\frac{2}{5} \right)\) et \(\displaystyle \left( \frac{3}{5},\frac{2}{5} \right)\). Or ces trois H-droites ne sont pas concourantes (se montre facilement). Il suffit alors de construire un triangle \(ABC\) avec un point sur chaque droite ainsi qu’un triangle\(A_1B_1C_1\) ayant ses côtés correspondants parallèles à ceux de \(ABC\) comme ci-contre pour illustrer que cette géométrie n’est pas arguésienne.
En pratique Hilbert ne va pas au delà dans l’analyse de son modèle non arguésien. Pour lui, il s’agit juste de montrer que cette géométrie existe. Nous nous proposons dans les pages suivantes d’explorer un peu plus en avant cette géométrie, et surtout de l’explorer dynamiquement.
Illustrations dynamiques de H-droites et H-triangles
En géométrie dynamique, une droite de base \((AB)\) se manipule à partir des deux points \(A\) et \(B\) qui la définissent, alors que dans le texte précédent de Hilbert les droites sont données en soi, sans référence à des points constituants. La différence est énorme puisque, pour la construction des H-droites définies par deux points, on peut distinguer trois cas :
• Cas 1 : les deux points sont extérieurs à l’ellipse.
• Cas 2 : les deux points sont intérieurs à l’ellipse.
• Cas 3 : un des points est à l’intérieur, l’autre à l’extérieur.
Dans les deux premiers cas, la construction de la H-droite \((AB)\) relève d’une construction géométrique élémentaire, mais le troisième cas, bien que n’étant a priori qu’un problème du 4° degré, est nettement plus complexe à traiter. S’intéressant dans ces pages plutôt aux illustrations des diverses propriétés, les détails techniques de construction de chaque cas – surtout le cas 3 – et la conjonction des trois cas sont abordés dans cet article.
Cette géométrie définie par Hilbert ne vérifie pas son axiome III.5
Elle ne vérifie pas la propriété de Desargues, car elle ne vérifie pas l’axiome III.5 sur les relations de congruence entre segments et angles.
Premier contact avec ce modèle : déplacer les points \(A, B\) et \(C\) à l’intérieur ou à l’extérieur de l’ellipse.
Préférer ouvrir cette première figure dans un nouvel onglet.
L’aspect non arguésien en version dynamique
On reprend le principe de l’illustration statique précédente. On part d’un triangle \(ABC\) et d’un point \(A_1\). Sur la parallèle à \((AC)\) passant par \(A_1\), on prend un point \(C_1\). La parallèle à \((BC)\) passant par \(C_1\) coupe la parallèle à \((AB)\) passant par \(A_1\) en un point \(B_1\). Puis on trace les trois droites \((AA_1), (BB_1), (CC_1)\) qui, en général, ne sont pas concourantes.
Cette figure nécessite plusieurs macro-constructions supplémentaires : la construction de la parallèle à une H-droite passant par un point, la construction d’un point sur objet d’une H-droite – qui peut être sur trois points différents – et l’intersection de deux H-droites, qui, elle, peut prendre la position de 5 points différents. La réalisation de ces macro-constructions, et de quelques autres (H-Longueur utilisée ci-dessus, H-milieu) est détaillée dans cet autre article. Cette figure est un peu particulière à utiliser, à cause du point \(C_1\), premier point sur objet d’une H-droite.
Le point \(M\) est l’intersection des droites \((AA_1)\) et \((CC_1)\) (vertes). On peut déplacer les points \(A, B, C\) et \(A_1\).
Le point \(C_1\) est directement manipulable quand il est à l’extérieur de l’ellipse,
et se manipule à partir de sa poignée (petit point rouge) quand il est à l’intérieur de l’ellipse.
La droite marron, \((BB_1)\), en général, ne passe par \(M\).
Préférer ouvrir cette figure dans un nouvel onglet.
Une version projective de la configuration de Desargues est proposée dans la page de construction des macros nécessaires à l’exploration de ce modèle. On peut aussi ouvrir cette figure ici.
Parallélogramme et H-milieux des diagonales
Ayant construit les parallèles et les milieux, on peut s’intéresser aux parallélogrammes – définis comme quadrilatères ayant ses côtés opposés parallèles – et aux milieux de leurs diagonales. Bien entendu, les diagonales ne se coupent pas en leurs milieux – sauf cas théoriques évidents, mais on peut trouver des configuration où cela peut être possible (comme l’illustration ci-dessous) … même si cela reste à explorer.
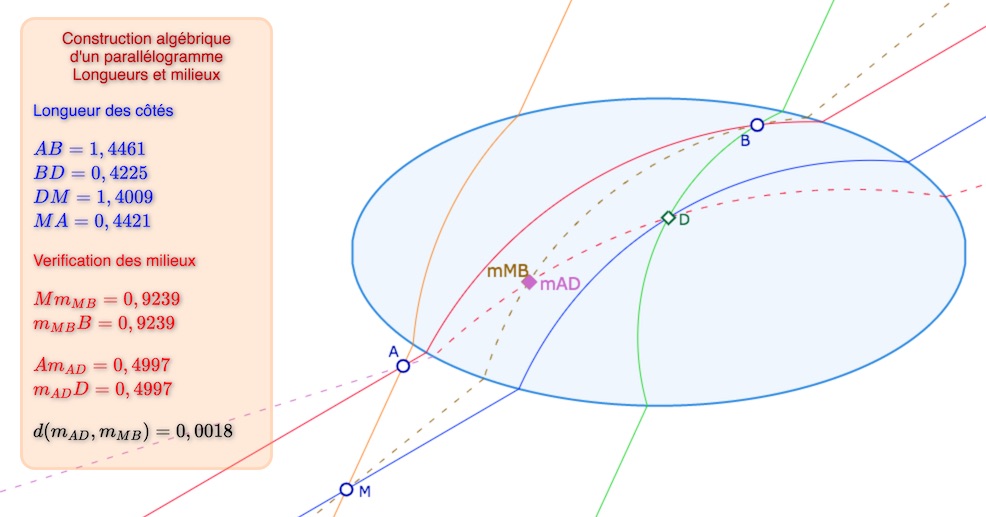
Ouvrir cette figure dans un nouvel onglet
Médianes d’un triangle
Bien entendu les médianes d’un triangle ne sont généralement pas concourantes. Nous montrerons à la page suivante, que, si les trois sommets sont dans l’ellipse, les médianes sont concourantes. Pour autant, on peut trouver de nombreuses configurations avec au moins un sommet hors de l’ellipse telles que les médianes soient néanmoins concourantes. Voici une galerie de 6 configurations où c’est le cas :
Six illustrations de concours des médianes hors de l’ellipse
On notera que deux illustrations ont les trois sommets hors de l’ellipse et donc les deux triangles \(ABC\),
l’euclidien et l’hilbertien, ont leurs médianes concourantes (en des points différents).
Comme il n’est pas possible, compte tenu de la complexité des expressions en jeu, de chercher un point de concours des médianes de manière algébrique et formelle, on va approcher un tel point par itérations successives, en déplaçant, d’une manière très fine, un des sommets du triangle. La précision est celle du JavaScript, soit au delà de \(10^{-13}\), et donc, pour une figure, bien au delà du millionième de pixel. Dans cette figure, on a construit deux points \(int_{AB}\) et \(int_{AC}\) des intersections des médianes prises deux à deux, et on cherche, par programmation Blockly du comportement du point \(B\), à rendre la distance entre ces deux point, nulle au sens informatique (\(d<10^{-13}\)).
Figure dynamique correspondante (peut prendre une dizaine de secondes à s’ouvrir)
En cas de difficulté, recharger la figure par l’icone de l’iframe. Éventuellement 2 fois.
Avec un peu d’habitude, la seconde option (maintenir le programme activé) s’avère efficace.
Penser aussi à désactiver le programme … pour voir qu’en général les médianes ne sont pas concourantes !
Ouvrir cette figure des médianes dans un nouvel onglet.
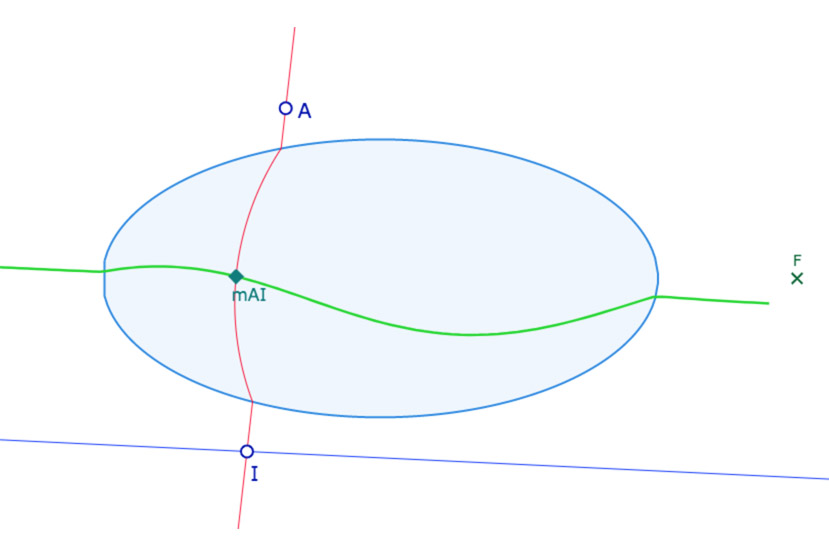
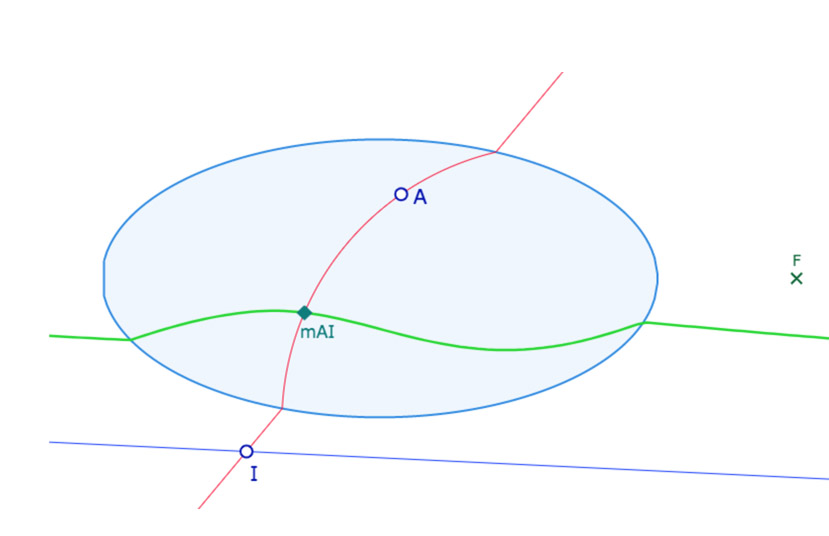
L’image du milieu d’un point fixe et d’un point sur une droite
En géométrie affine, ce lieu est la droite des milieux d’un triangle, parallèle au côté. Dans la géométrie non arguésienne de Hilbert, ce lieu n’est pas une droite. Voici un galerie de 9 illustrations.
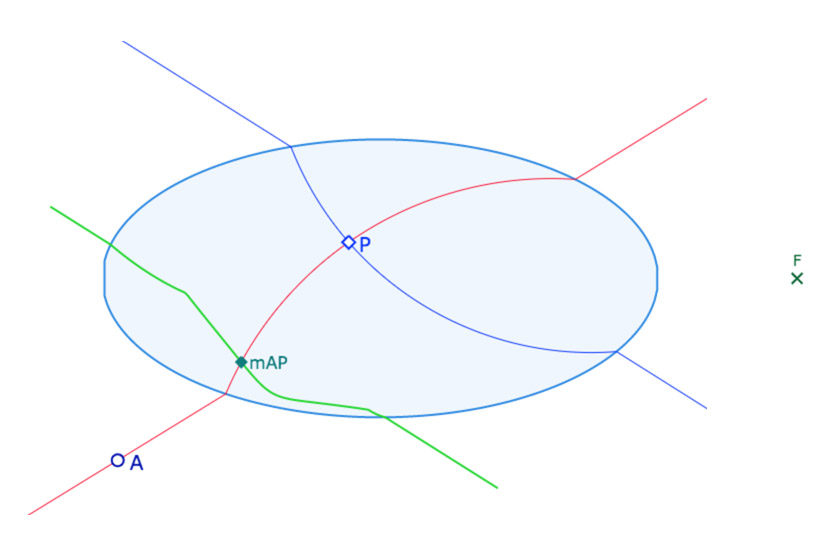
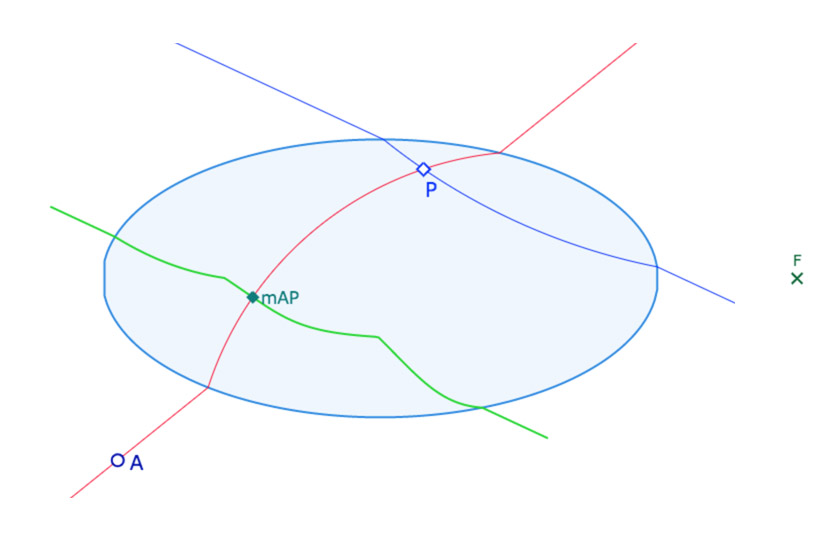
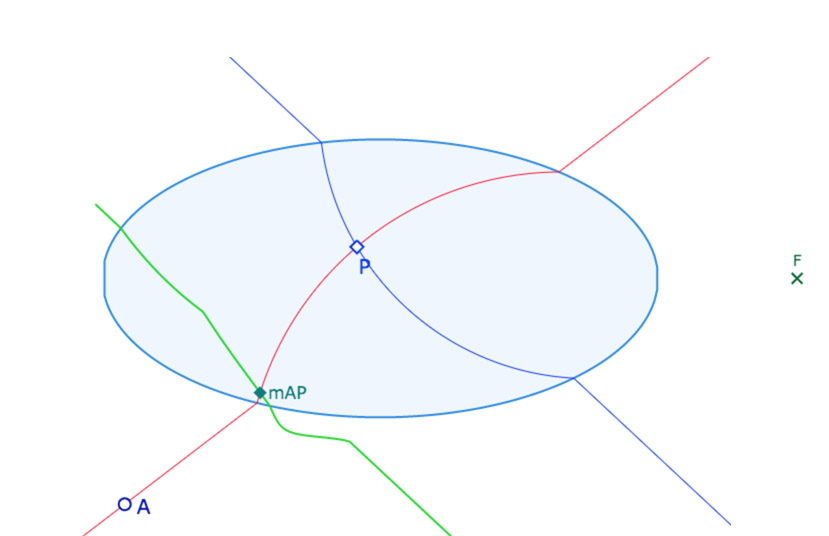
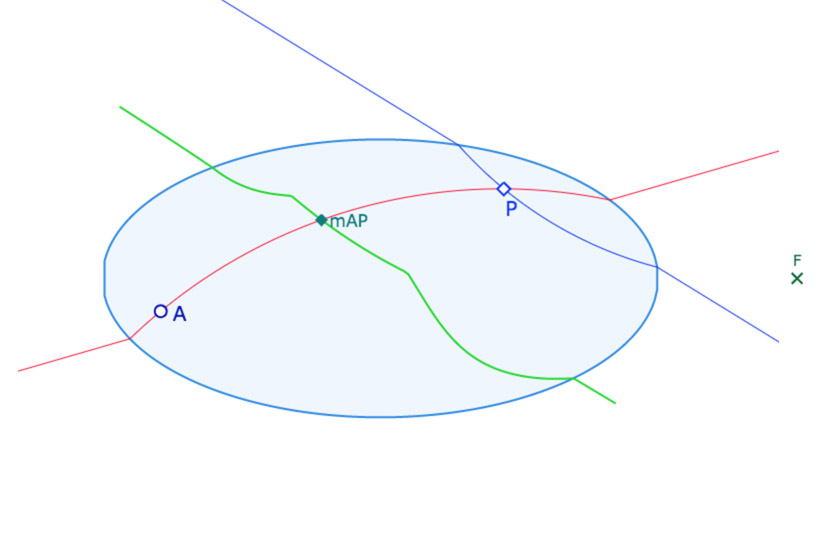
En vert le lieu du milieu des points \(A\) et \(I\) ou \(P\) quand ces points parcourent la droite \((MN)\) (\(I\) quand \((MN)\) est extérieure à l’ellipse, \(P\) quand \((MN)\) coupe l’ellipse.
Les figures associées
Deux figures, pour distinguer deux cas (pour rendre le lieu plus manipulable), celui où la droite support est extérieure à l’ellipse et celui où elle coupe l’ellipse.
• la figure Lieu_Milieu_DrtEx : la droite (MN) qui ne doit pas couper l’ellipse.
• la figure Lieu_Milieu_DrtInt : la droite (MN) qui doit couper l’ellipse.
Attention, si la première droite s’ouvre très vite, la seconde peut mettre, selon votre processeur, deux à trois minutes pour s’ouvrir. Une fois ouverte, la figure reste fluide, manipulable par les points \(M, N\) et \(A\).