Le contexte ici est différent de la page précédente, et plus simple à traiter. Dans cette page, on se donne une H-droite \((AB)\) avec \(A\) et \(B\) à l’intérieur de l’ellipse, et un point \(M\), lui aussi à l’intérieur de l’ellipse. Le régionnement de l’ellipse consiste à colorier les cas où il n’y a aucune perpendiculaire, deux perpendiculaires – dans ce cas c’est une hibertienne et une euclidienne car il ne peut y avoir deux hilbertiennes, et le cas où il n’y a qu’une seule perpendiculaire euclidienne.
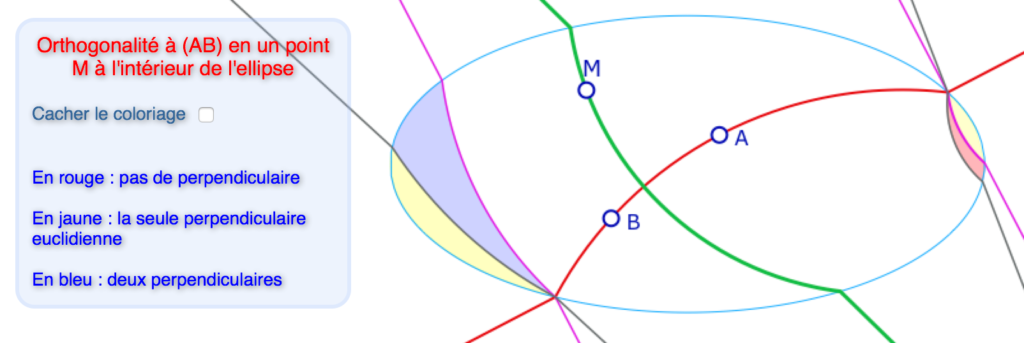
On a choisi de ne pas colorier le cas le plus trivial, celui où il n’y a qu’une perpendiculaire hilbertienne car c’est, en général, la plus grande partie à l’intérieur de l’ellipse comme on le voit sur cette illustration. La H-orthogonalité est l’orthogonalité euclidienne de deux cercles : celui circonscrit à \(A, B\) et \(F\) et celui passant par \(M, F\) et orthogonal au précédent.
Les trois autres régions sont des parties de l’ellipse qui partent de ses points d’intersection avec la H-droite \((AB)\).
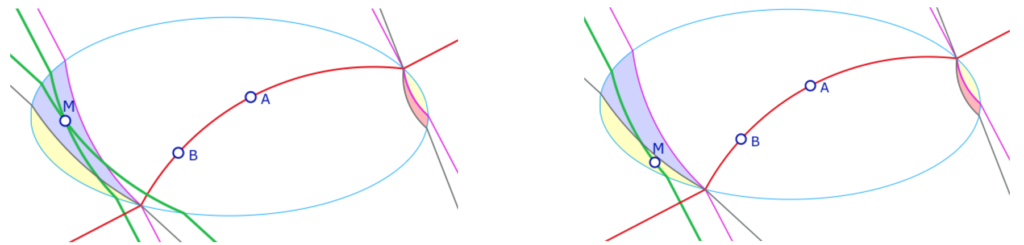
La partie à une seule perpendiculaire euclidienne peut être assez importante, ici avec deux droites \((AB)\) différentes.

En fait la figure finale n’est pas très opérationnelle … elle n’est correcte qu’à 60% des cas. La rédaction a été annulée et fait partie des prochaines mises à jour ….
Un peu désolé … mais temporaire …
Intro orthogonalité | H-ortho 1 (triangles) | H-ortho 2 (régionnement extérieur) | H-ortho 3 (régionnement intérieur)