Retour à la page de définition générale des droites du modèle de Hilbert
Dans cette page, on aborde les sujets suivants :
• Tout d’abord, on traite du troisième cas, la construction de la droite \((AB)\) quand elle est définie par un des points extérieur à l’ellipse et l’autre intérieur à l’ellipse.
• En même temps, on présente succinctement la concaténation des trois cas.
• Enfin on aborde la construction des droites parallèles, dans le cas général avec comme applications
– la construction la plus générale possible d’un parallélogramme
– puis de la configuration de Desargues.
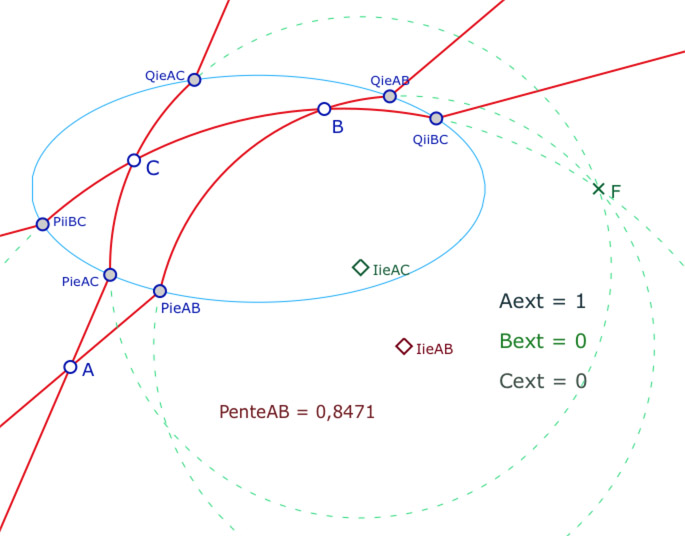
Désignation des points : on utilise trois préfixes, selon les trois cas de positionnement des points de base par rapport à l’ellipse. Pour les points d’intersection avec l’ellipse on note :
• \(P_{ie}\) pour un des points à l’intérieur et l’autre extérieur
• \(P_{ii}\) : les deux points sont à l’intérieur de l’ellipse
• \(P_{ee}\) : les deux points sont à l’extérieur (cas 1 non illustré ci-contre).
• On utilise les noms des droites comme suffixe.
Pour construire cette H-droite \((AB)\) il faut déterminer les intersections \(P_{ieAB}\) et \(Q_{ieAB}\) de l’arc de cercle passant par \(B\) et \(F\) tel que les trois points \(A\), \(P_{ieAB}\) et \(Q_{ieAB}\) soient alignés. Il faut donc trouver le centre \(I_{ieAB}\) de ce cercle, sur la médiatrice de \([BF]\) tel que les pentes des deux droites \((AP_{ieAB})\) et \((P_{ieAB}Q_{ieAB})\) soient de même pente.
Même si ce n’est, a priori, qu’un problème d’ordre 4, sa résolution formelle – à savoir trouver les coordonnées du centre \(I_{ieAB}\) en fonction de celles, dynamiques, de \(A\) et \(B\) est trop longue (plus de 10000 caractères) pour être introduite dans le logiciel. On devrait pouvoir la simplifier, mais ce travail n’a pas été fait, on a choisi une autre piste.
La programmation de la H-droite générale
Dans cette page – ce site pour le moment – on s’en est tenu à une solution approchée obtenue par dichotomie, avec une précision de l’ordre du dix-millième de pixel, ce qui permet, en pratique, d’atteindre une précision écran identique à une « solution exacte », et permet une illustration dynamique fiable de cette géométrie et l’exploration des premières propriétés comme déjà vu pour les deux premiers cas. Voici quelques détails techniques de cette construction.
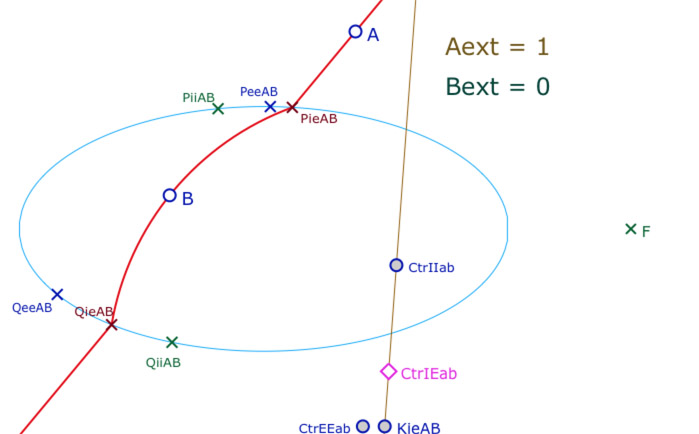
Le centre \(CtrIE_{ab}\) du cercle cherché (passant par \(P_{ieAB}\), \(Q_{ieAB}\) et \(B\)) est sur la médiatrice de \(B\) et\(F\). Une première exploration montre que ce point est entre le projeté horizontal \(K_{ieAB}\) du centre du cercle du cas 1, \(CtrEE_{ab}\), où les deux points sont considérés comme extérieurs à l’ellipse, et le centre \(CtrII_{ab}\), lui sur la médiatrice, du cercle solution du cas 2, quand les deux points sont intérieurs. Ces bornes sont les points \(IminAB\) et \(ImaxAB\) des premières lignes du code Blockly suivant.
Les booléens \(Aext\) et \(Bext\) indiquent si les points sont intérieurs ou extérieurs à l’ellipse et le point \(ABext\) est celui des deux qui est à l’extérieur.Un premier choix du point \(CtrII_{ab}\) permet de construire le cercle qui coupe l’ellipse en \(P_{ieAB}\) et \(Q_{ieAB}\). Le nombre \(pPQ\) calcule la pente de la droite passant par ces points (avec les noms \(Pg_{AB}\) et \(Qg_{AB}\)) et le nombre \(pPextP\) est la pente entre le point extérieur et un point d’intersection avec l’ellipse. Puis on itère 20 fois l’algorithme de dichotomie.
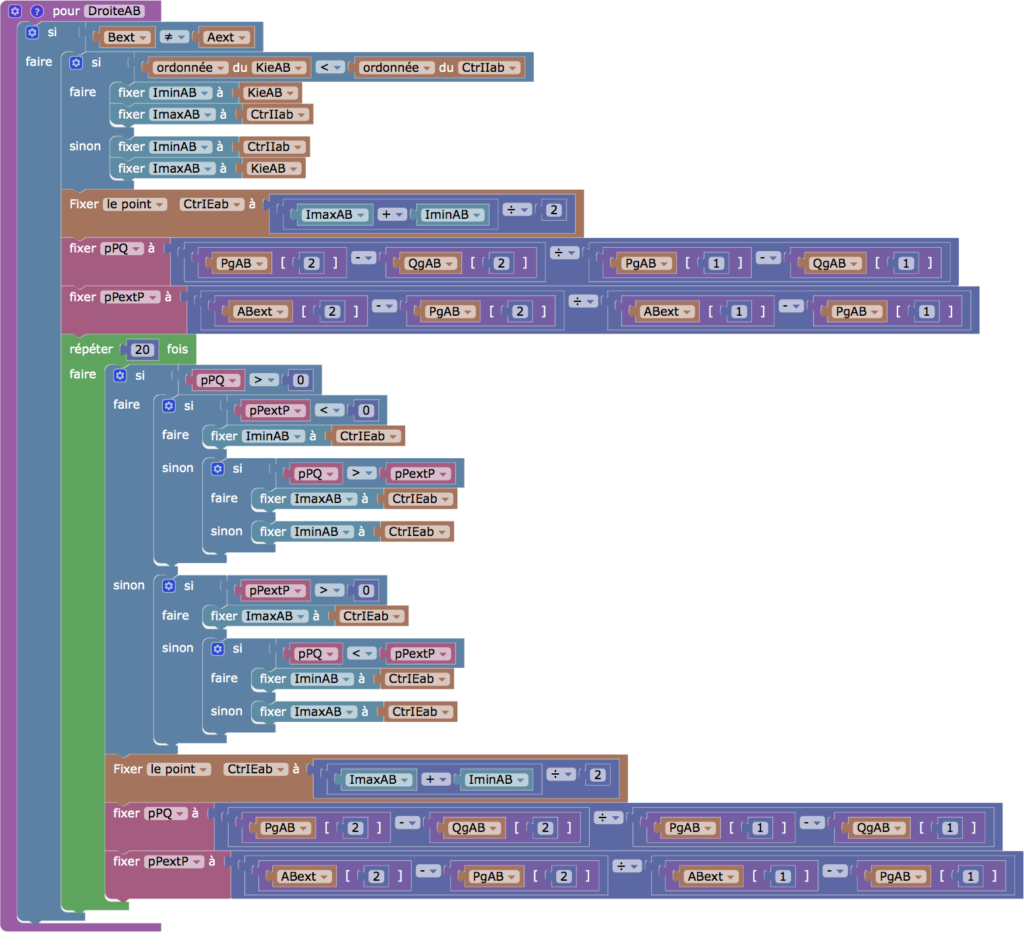
On utilise ici pleinement l’aspect comportement du Blockly de DGPad : dans la boucle le point \(CtrIE_{ab}\) est mis à jour (par l’instruction Fixer) ce qui met à jour les points d’intersection \(Pg_{AB}\) et \(Qg_{AB}\) et permet ainsi d’itérer sur les mêmes points.
La figure suivante est une figure de démonstration où le nombre d’itérations est variable (curseur n) pour voir la précision des pentes en fonction du nombre d’itérations comme illustré dans ces trois exemples :
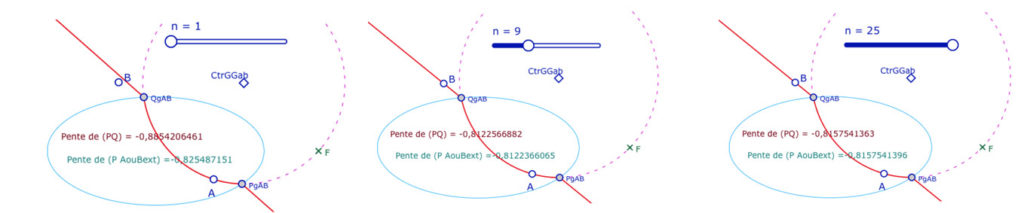
Concaténation des trois cas
Pour une plus grande souplesse « utilisateur », la figure proposée contient déjà la concaténation des trois cas. C’est pourquoi le centre s’appelle \(CtrGG_{ab}\) tout comme les points d’intersection de la H-droite avec l’ellipse. Cette concaténation des trois cas est construite par combinaisons linéaire booléennes de chacun des trois points, ceux d’indice \(ee\) (cas 1), ceux d’indice \(ii\) (cas 2) et ceux construits ici d’indice \(ie\) (cas 3) :
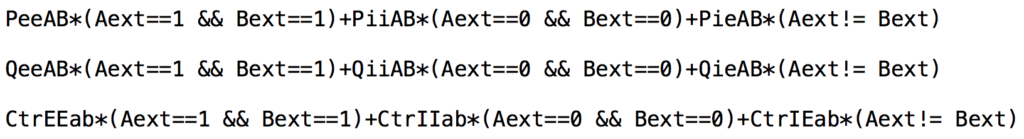
Dans cette figure on peut faire passer les points de base de l’intérieur à l’extérieur de l’ellipse.
Le curseur n’a de sens que si un point est à l’intérieur et l’autre à l’extérieur.
Ouvrir une autre figure sur la définition générale de la H-droite dans un nouvel onglet. (toujours avec le curseur d’exploration, et sans les restrictions de l’iframe).
Parallélisme dans le modèle de Hilbert
L’objectif de la fin de cette page est essentiellement la construction d’une figure dynamique de la configuration de Desargues dans le cadre le plus général. Aussi modeste qu’elle soit, cette construction n’est pas triviale puisqu’il faut construire 9 droites, dont trois droites parallèles (sur la base de la configuration dite « affine »). On commence donc par le parallélisme.
On s’intéresse à la construction de la parallèle à la droite \((AB)\) passant par un point \(A_1\). Il y a d’abord les cas simples, comme dans l’illustration de gauche, où \(A\) et \(B\) sont tous les deux intérieurs ou extérieurs à l’ellipse. SI \(A_1\) est extérieur à l’ellipse, la construction de la parallèle est géométrique (donc productible par une macro-construction). Dans ce cas les deux pentes des droites, par construction, sont égales.
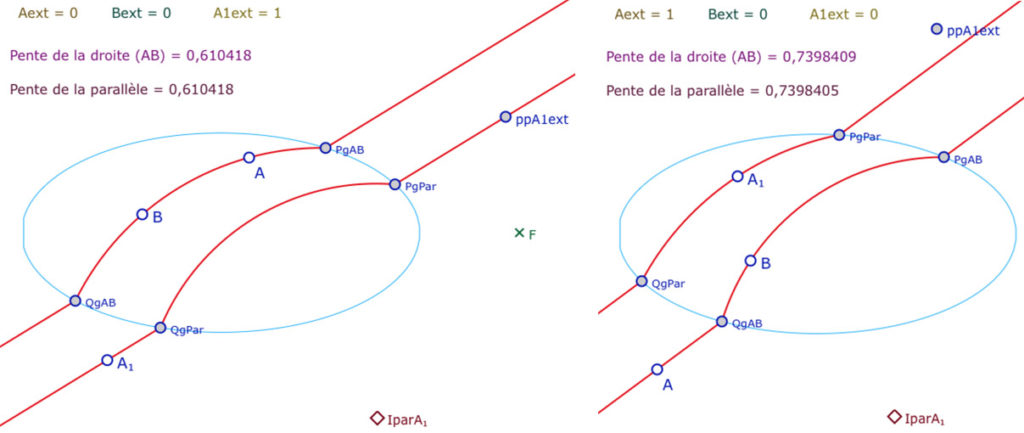
Le cas général le plus délicat est celui représenté par l’illustration de droite où la droite \((AB)\) est déjà construite par programmation et, quand \(A_1\) est intérieure à l’ellipse.
La droite parallèle est alors construite avec la même démarche de dichotomie pour placer les points \(Pg_{par}\) et \(Qg_{par}\). Dans ce cas les deux pentes sont égales à \(10^{-6}\) voir \(10^{-7}\) près.
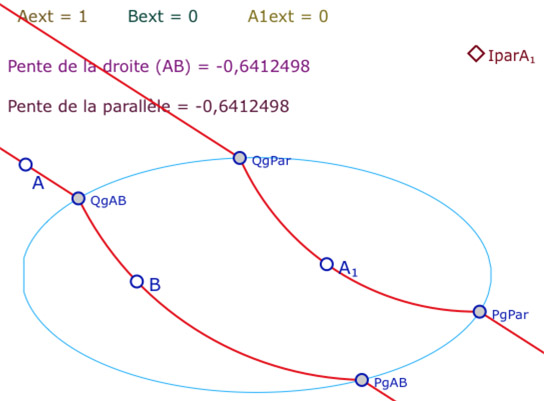
La valeur numérique de la pente de la parallèle à \((AB)\) par \(A_1\), obtenue par dichotomie peut être très précise comme ci-contre.
Aspects techniques de la construction
En fait, pour que l’on puisse utiliser les droites parallèles assez généralement, il faut modifier les définitions des points d’intersection avec l’ellipse \(Pg_{par}\) et \(Qg_{par}\) et transformer la simple combinaison linéaire des points \(P_{ii}, P_{ie}, P_{ee}\) en une forme moins linéaire – et pourtant logiquement équivalente – alors que le centre générique de l’arc de la parallèle à l’intérieur de l’ellipse, reste une combinaison linéaire du centre obtenu par programmation (\(I_{parA_{1}}\)) et du centre construit géométriquement (\(Ctre_{par} \)). En voici les expressions :
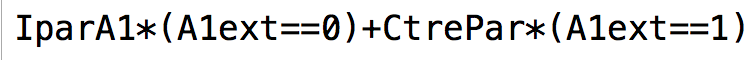

Mise en œuvre pratique
Pour la construction des droites et des parallèles, la procédure est :
• Utiliser d’abord les macros constructions (aspect géométrique des cas 1 et 2)
• Ajouter sur le centre (\(IieAB\) ou \(I_{parA_{1}}\)) le code blockly de dichotomie – présenté plus haut – en adaptant manuellement les variables en fonction de la situation.
On comprend bien que la construction de 9 droites générales pour la configuration de Desargues produise une figure assez lourde. Arriver à finaliser la construction générale algébriquement serait un vrai progrès pour aller plus loin dans l’exploration du modèle de Hilbert … avis aux amateurs …
Les macros HDroite Gene renvoient tous les objets nécessaires avec leur gestion de cache intégrée. Voici par exemple ce que retournent la première (Détails) et la seconde (min net) :

Manipulations sur une figure de base
Construction d’un parallélogramme générique
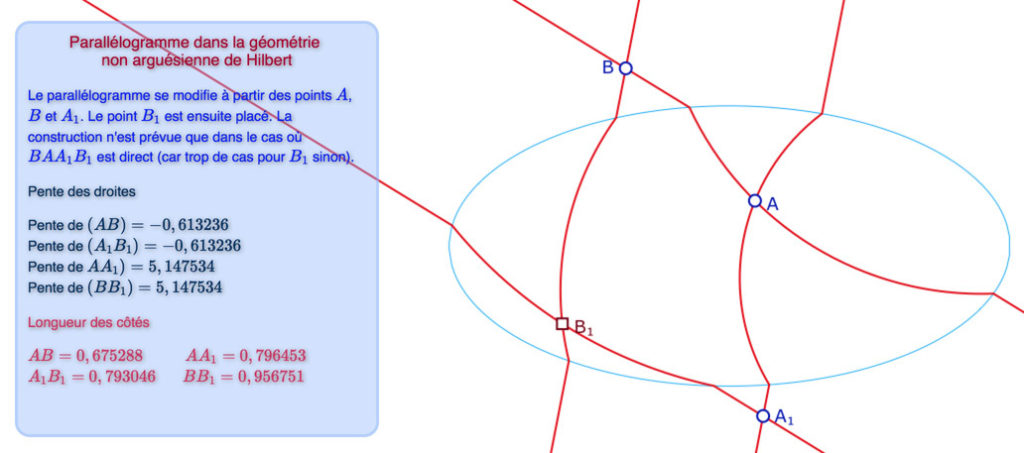
Voici un parallélogramme dans la configuration la plus générale puisque pour chaque droite il y a un point à l’intérieur et un point à l’extérieur de l’ellipse (et donc nécessitant l’utilisation de la partie programmation pour les 4 droites.
La longueur est la longueur euclidienne du H-segment, en général composé d’un arc de cercle et d’un segment. Tous les cas sont traités dans la fonction HLongueur, sauf le cas où le segment ne coupe pas l’ellipse, quand c’est un simple segment euclidien. Comme il n’y a pas de bloc NaN on doit utiliser à part une Expression pour traiter ce cas avant d’appliquer la fonction.
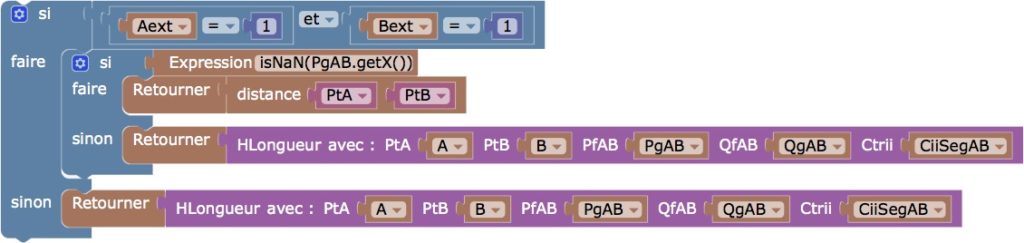
Les paramètres de la fonction HLongueur sont les deux points, les intersections de la droite avec l’ellipse – d’où la nécessité de traiter en amont le cas où ces intersections n’existent pas – et le centre de la partie «arc de cercle» de la droite. On n’a pas reproduit le code, long car un peu technique, mais sans complexité particulière. Un lecteur intéressé le retrouvera dans les figures.
Pour le calcul de la longueur, on traite tout simplement trois cas distincts. D’abord si les deux points sont à l’intérieur de l’ellipse, ce n’est qu’un calcul d’arc d’une ligne. Puis si les deux sont à l’extérieur, on fait simplement la somme des longueurs à l’extérieur et de celle à l’intérieur de l’ellipse, chacune étant simple à calculer.
Seul le cas où un point est intérieur et l’autre extérieur demande un peu d’attention pour une gestion dynamique.
Manipulation de la figure « parallélogramme avec longueur des côtés »
On peut agir sur les points \(A, B, A_1\) en les plaçant à l’intérieur ou à l’extérieur de l’ellipse.
Les pentes sont mesurées en temps réel, ce qui permet de vérifier le «parallélisme» des droites.

On peut aussi choisir d’ouvrir la figure sans restriction dans un nouvel onglet.
Le lecteur intéressé par la programmation peut alors regarder le code de HLongueur.
Pour cela il faut faire apparaître (avec l’outil gomme) l’expression distAB et ouvrir le Blockly de cette expression (dernière icone à droite). A éviter dans la figure de cette page car il faut plus de place.
On se propose désormais d’ajouter les milieux des diagonales et leurs milieux. La figure peut être plus longue à venir à cause du calcul de la position des milieux. Il peut falloir recharger la page. C’est la raison pour laquelle on a présenté deux figures pour le parallélogramme.
La figure est stable, mais il faut au départ déplacer le point \(B\) pour activer les calculs des milieux qui sont dans le point \(B\).
Ouvrir cette même figure dans un nouvel onglet.
La configuration de Desargues
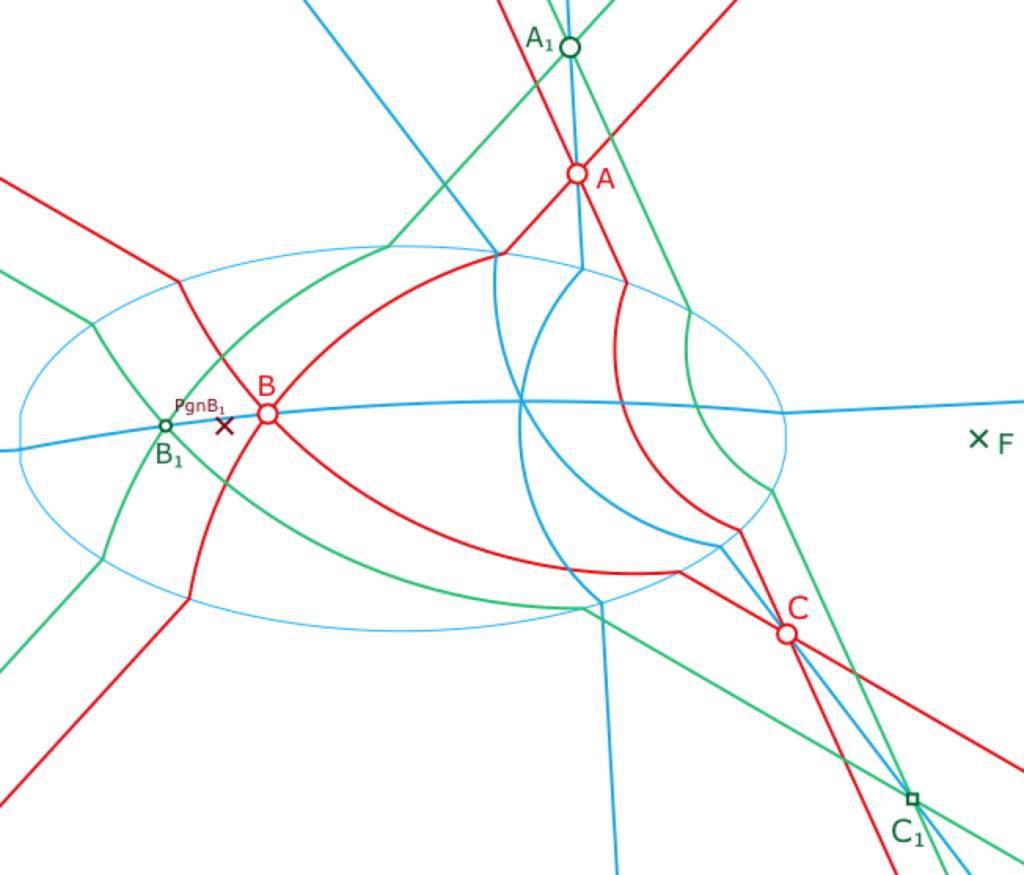
Ayant réalisé la construction générale d’une parallèle à une droite passant par un point, on peut désormais s’intéresser à une figure générale de la configuration de Desargues.
On se donne un triangle \(ABC\) (droites rouges), et un point \(A_1\). On commence par construire les parallèles à \((AB)\) et \((AC)\) passant par \(A_1\) (droites vertes).
Sur la parallèle à \((AB)\) passant par \(A_1\), on prend un point \(B_1\). Alors, la parallèle à \((BC)\) passant par \(B_1\) (troisième droite verte) coupe la parallèle à \((AC)\) passant par [\(A_1\) en un point \(C_1\).
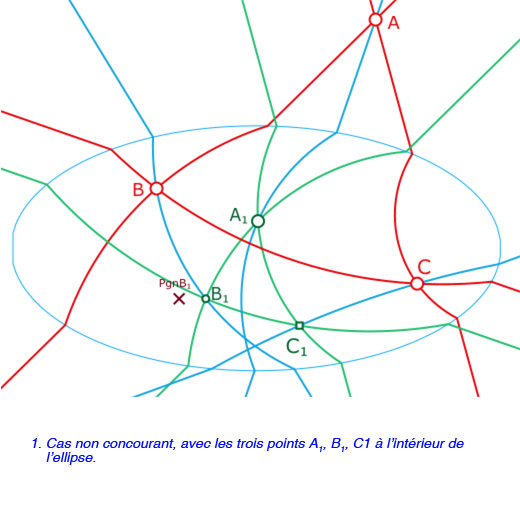
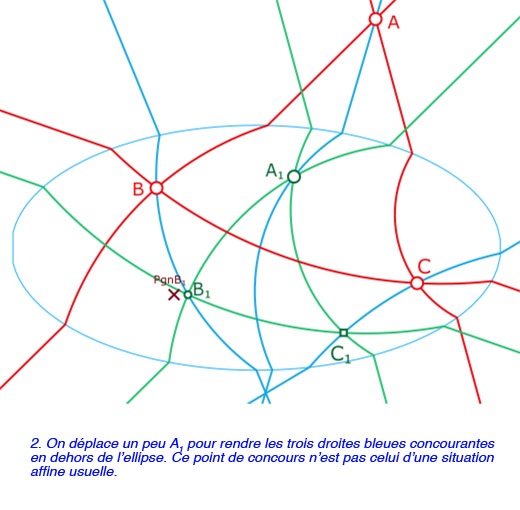
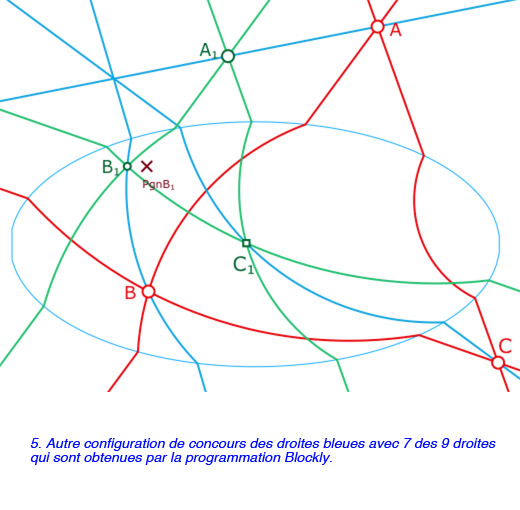
Le théorème de Desargues est vérifié si les droites \((AA_1), (BB_1), (CC_1)\) sont (toujours) concourantes comme c’est le cas – mais en pratique assez exceptionnel – dans l’illustration ci-contre.
Pour que le point \(B_1\) puisse être pris sur toute la H-parallèle à \((AB)\) passant par \(A_1\) (en pratique soit sur un arc de cercle, soit sur une demi droite), on le pilote par une poignée, le point \(PgnB_1\) qui lui appartient à une droite euclidienne. \(B_1\) est simplement le projeté horizontal de sa poignée sur sa H-droite.
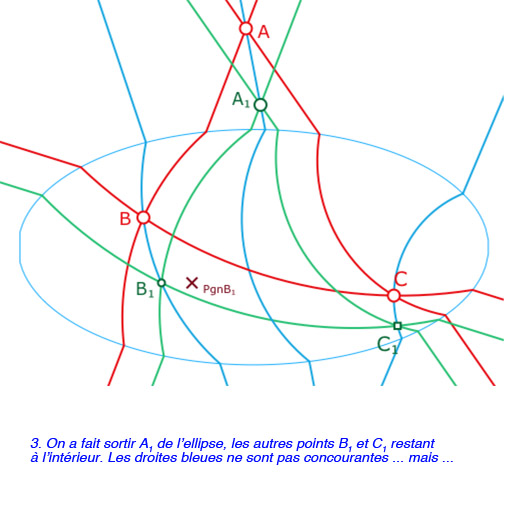
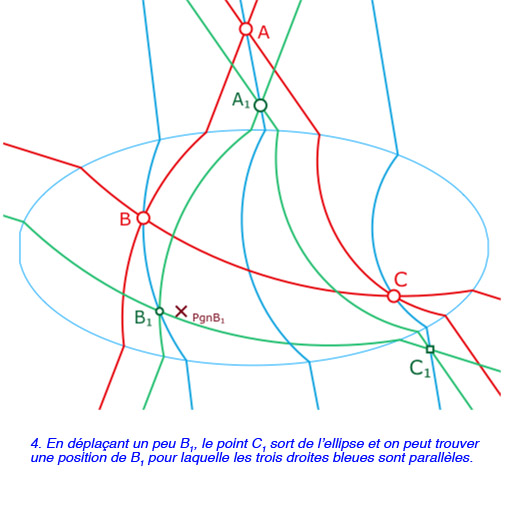
La construction de \(C_1\) est une simple combinaison linéaire booléenne des points d’intersections possibles entre les différentes options, selon la nature des droites et les parties de ces droites. Même si c’est théoriquement élémentaire, cela reste pourtant, d’un point de vue dynamique, la partie la plus fragile de la construction.
Quelques exemples de situations de la configuration de Desargues «affine» dans le contexte du modèle de Hilbert.
On observera qu’il faut construire 9 H-droites comprenant toutes une partie de programmation (dynamiquement utilisée ou non selon la configuration).
Dans certains cas, il devrait pouvoir être abordable, pour \(A, B, C\) et \(A_1\) fixés, de calculer la position exacte de \(B_1\) qui rend les trois droites \((AA_1), (BB_1)\) et \((CC_1)\) concourantes. La galerie ci-dessous propose simplement quelques exemples d’approximations visuelles obtenues par les programmations précédentes largement réalistes (précision à au moins \(10^{-6}\) .
Galerie de 5 exemples de la configuration de Desargues dont des cas particuliers qu’il serait intéressant d’étudier plus profondément.
La figure associée
Cette figure est nettement plus complexe que toutes les précédentes.
Elle est moins réactive mais aussi, hélas, moins stable, en particulier pour le placement de \(C_1\).
Ne pas hésiter à la relancer par l’icone spécifique de l’iframe.
Ouvrir la même figure en plein écran, sans restriction, dans un nouvel onglet.