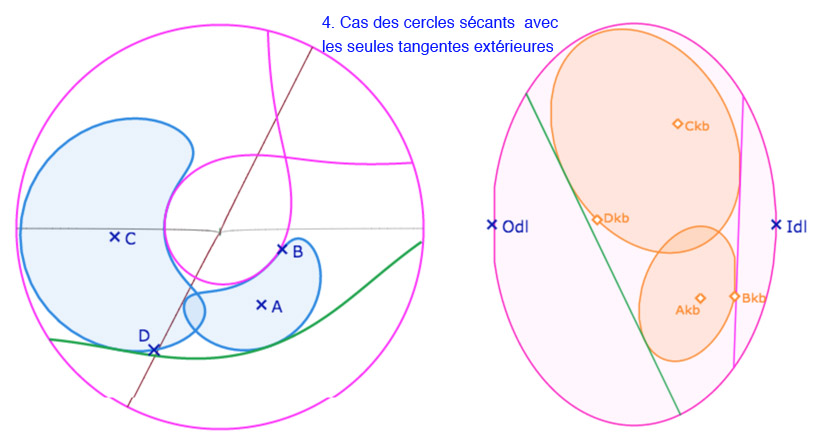
Cercles exinscrits sur la pseudosphère
Dans la figure suivante, un peu exceptionnellement, on a limité les droites à la feuille principale. En effet, dans beaucoup de situation au moins une bissectrice est proche d’un méridien et s’enroule plusieurs fois sur la pseudosphère, rendant la figure assez illisible.
Cette figure ne traite que des cercles exinscrits, pas des cycles exinscrits en général.
Comme pour les autres figures, on peut agir sur les sommets et leurs latitudes, et tourner la pseudosphère.
Préférer ouvrir la figure dans un nouvel onglet
Le rêve de Coxeter
On se propose dans ce paragraphe d’illustrer une phrase un peu malheureuse de Coxeter dans la seconde édition de son ouvrage « Introduction à la géométrie » où il laisse entendre que les géodésiques de la pseudosphère qui ne sont pas des méridiens s’enroulent indéfiniment autour de la surface (p. 378) :

Une courbe qui s’enroulerait à l’infini en montant dans une même direction ?
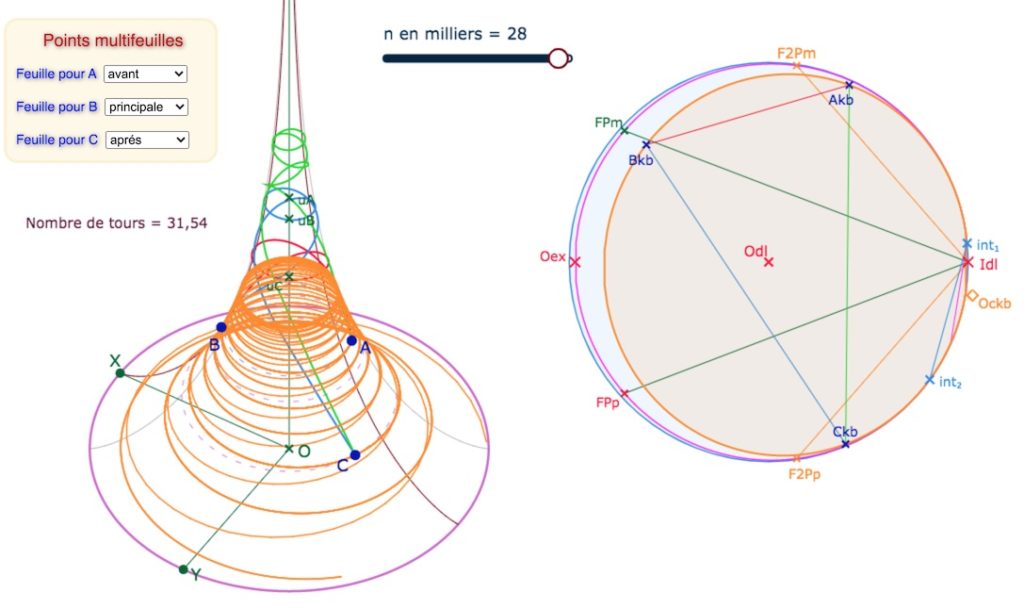
C’est intéressant de relever le défi de construire une courbe qui vérifie ce qu’on a choisi d’appeler « le rêve de Coxeter », à savoir s’enrouler sur la pseudosphère indéfiniment en s’élevant en altitude. Pour cela il faut tendre vers le seul point idéal de la pseudosphère. Cela ne peut pas être une droite, car les seules droites qui vont vers l’infini sont les méridiens qui ne s’enroulent pas. Cela ne peut pas être ni un cercle, ni même un horicycle car les seuls horicycles qui ont pour centre le point idéal \(I_{dl}\) correspondent aux parallèles à l’équateur : ils s’enroulent bien indéfiniment, mais pas en augmentant d’altitude. On peut donc chercher les conditions pour qu’une équidistante soit solution. Voici ce qu’on se propose de réaliser :
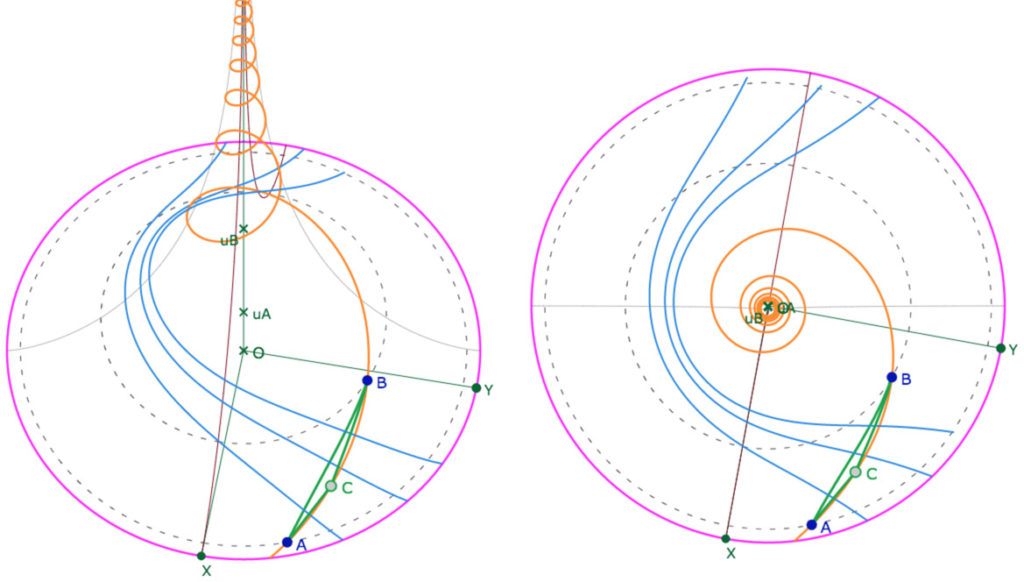
Dans cette figure, les médiatrices bleues du triangle \(ABC\) (\(C\) construit) admettent comme équidistante
une courbe qui correspond à ce que l’on attend : le rêve de Coxeter est réalisé.
Le principe de la réalisation
On a vu dans l’item précédent sur le modèle KB que, dans ce modèle, une équidistante est une ellipse bi-tangente au cercle-limite. Pour que l’équidistante s’enroule indéfiniment, il faut – et il suffit – que l’un de ces points de contact de cette ellipse soit le point idéal. C’est ce que nous allons réaliser maintenant.
Depuis deux points \(A\) et \(B\) de la pseudosphère sont envoyés en \(A_{kb}, B_{kb}\) sur le disque limite. On construit alors la perpendiculaire passant par le point idéal \(I_{dl}\) à la médiatrice de \([A_{kb}B_{kb}]\). Sur cette droite, on prend un point \(H\) et de ce point on prend la perpendiculaire au méridien qui est alors la perpendiculaire comme entre cette droite et la médiatrice. On construit alors \(C_{kb}\) le symétrique de \(A_{kb}\) par rapport à cette droite. Le triangle \(A_{kb}B_{kb}C_{kb}\) est un triangle dont les trois médiatrices sont en faisceau à axe dont l’axe est un méridien. Le triangle est donc sur une équidistante dont le point \(I_{dl}\) est un des points idéaux : il est donc accessible sur la pseudosphère : c’est la courbe que nous construisons
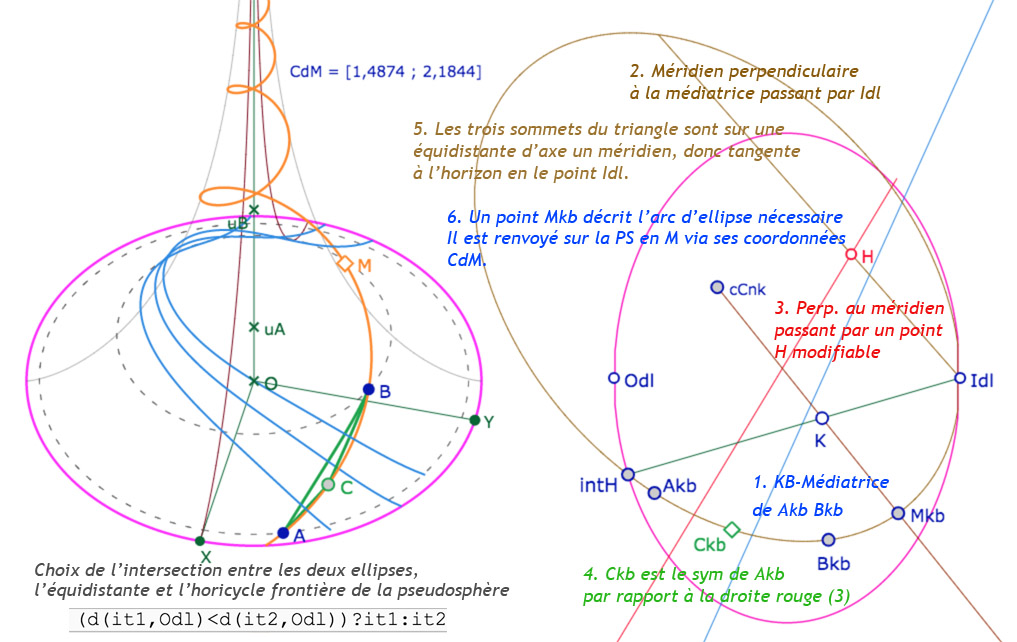
Version illustrée des différentes étapes
Ci-dessous une illustration d’une équidistante plus resserrée avec des médiatrices multifeuilles
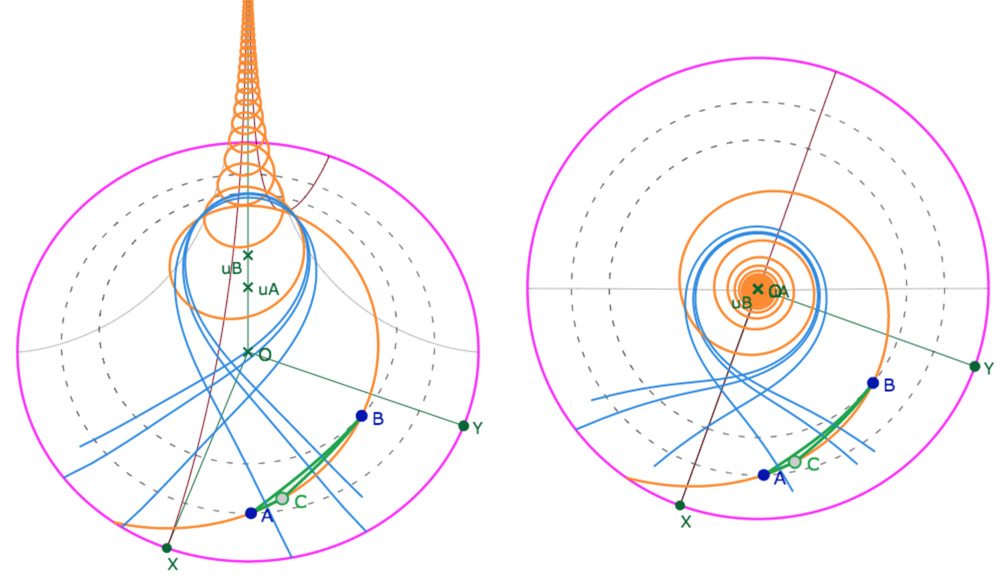
La figure est un peu lourde pour être placée dans cette page, d’autant qu’il est préférable d’avoir un écran dédié vu la taille de la figure.
Attention, être patient : elle peut mettre une quinzaine de seconde avant de s’ouvrir ! L’ouvrir ici.
Tangentes communes à deux cercles sur la pseudosphère
Les tangentes communes à deux cercles est une application classique des centres d’homothéties des deux cercles puisque ce sont les tangentes à un des deux cercles issues des deux centres d’homothéties de ces cercles. Mais dans un contexte hyperbolique, il n’y a pas d’homothétie, et donc pas de centres d’homothéties. La construction doit donc être nécessairement différente. Pour cela on peut, une nouvelle fois, utiliser la conjugaison en faisant la construction des tangentes communes des images des deux cercles.
Ces images étant deux ellipses, la question est alors celle de la possibilités, par les logiciels contemporains, de construire les tangentes communes à deux coniques. On se propose de le faire de manière géométrique puis les KB-droites sont des segments, et donc les tangentes communes sont les mêmes en géométrie euclidienne et dans le modèle de Klein Beltrami pour la géométrie hyperbolique.
Tangente commune à deux coniques par polaire réciproque
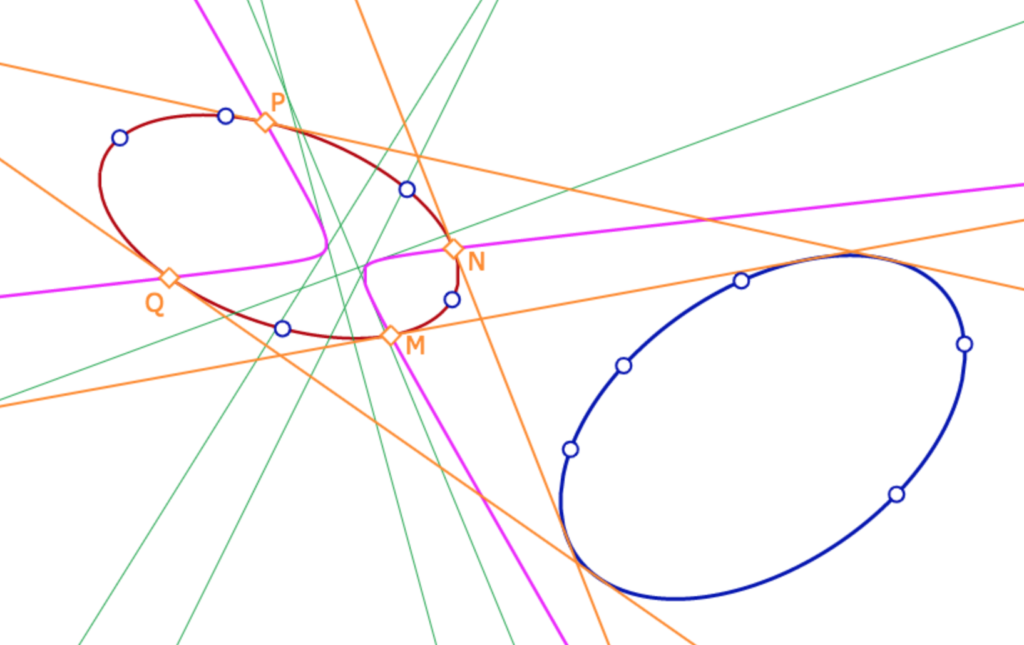
Étant données deux coniques, ci contre la bleue et la rouge, le principe est d’en transformer une par polaire réciproque par rapport à l’autre . La transformation est ponctuelle mais comme une conique est définie par 5 points il suffit de faire la transformation pour ses 5 points constituants. En pratique on construit les 5 polaires des points constituants de la conique bleue par rapport à la conique rouge. On obtient les 5 droites droites vertes ci-contre. La transformation par polaire réciproque de la conique bleue (par la rouge) est la conique rose construite de manière tangentielle, à partir de ses 5 tangentes (et donc les droites vertes).
Alors la propriété qui nous intéresse ici est que l’intersection de la conique de référence pour la transformation (la rouge) avec la transformée de la bleue (l’hyperbole rose) sont les points de contact, sur la conique de référence, des tangentes communes aux deux coniques. Il suffit alors de construire, sur la conique de référence, les tangentes en ces points pour avoir la tangente commune.
Retour sur la pseudosphère
La construction précédente étant transformée en macro-construction, on l’applique dans KB sur les cercles images des cercles de la pseudosphère. Et on renvoie ces droites. En pratique, la transformée de l’ellipse étant une hyperbole, les intersections des deux coniques ne sont pas stables au sens où il n’y a pas un suivi continu des intersections : si on les numérote, ces numéros sautent de l’un à l’autre dés qu’on bouge un peu une des coniques.
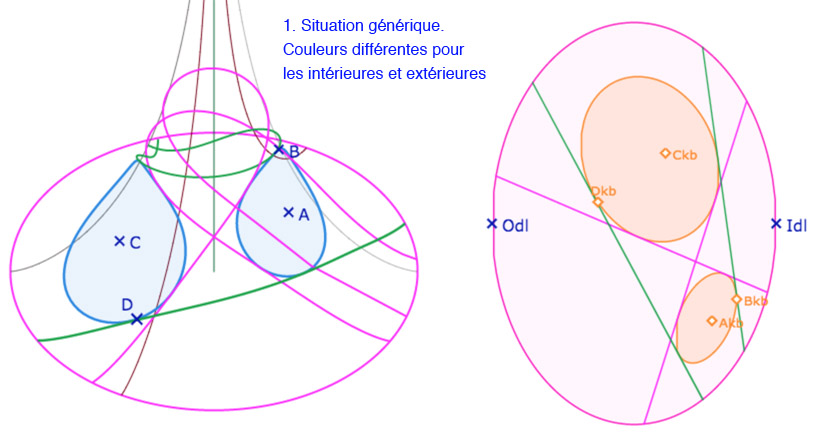
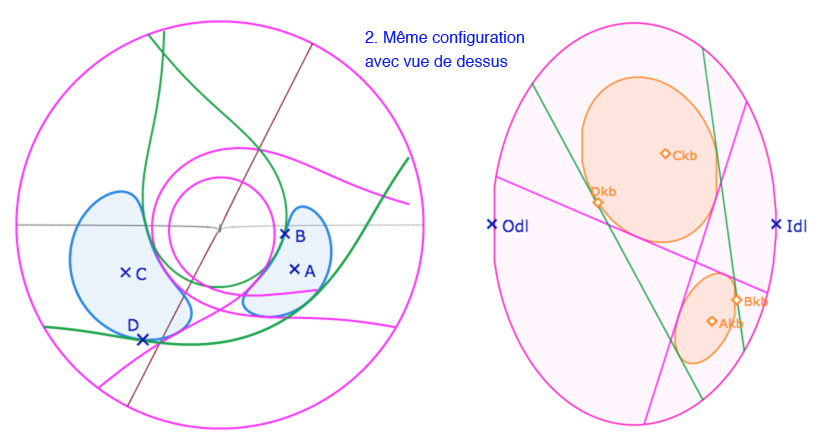
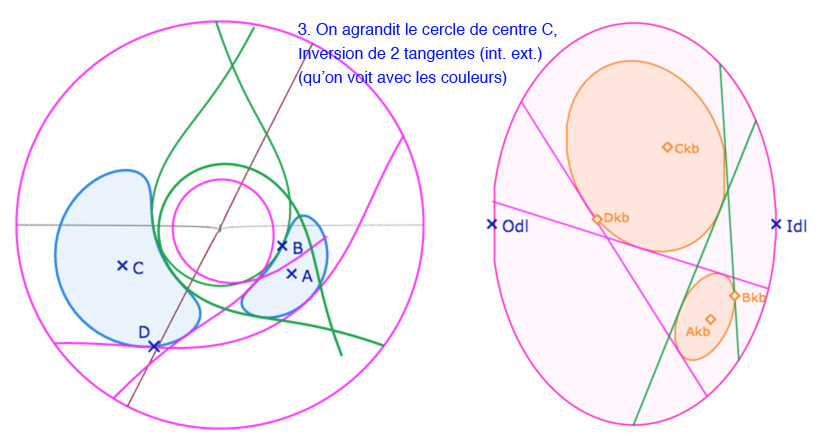
Illustration du résultat
Galerie de 4 illustration vue de face ou de dessus
La figure associée
Utiliser par exemple le fait de voir sur KB si une tangente entre dans une autre feuille pour ajuster les points du cercle sur la pseudosphère.
Remarque : dans cette figure aussi l’orientation de la pseudosphère ne se modifie pas au doigt ou au clic de la souris. Il faut donc un clic droit à la souris ou deux doigt sur tablette dont un appuyé et l’autre qui glisse.
Les tangentes ne sont pas toujours stables quand les cercles sont petits ou proches des feuilles adjacentes à la principale
Préférer ouvrir la figure « hors restriction » dans un nouvelle onglet
Malfatti de trilatère sur la pseudosphère
Et bien entendu, parce que cette figure est une sorte de fil rouge de ce site, voici la version pseudosphérique de la construction de Malfatti.
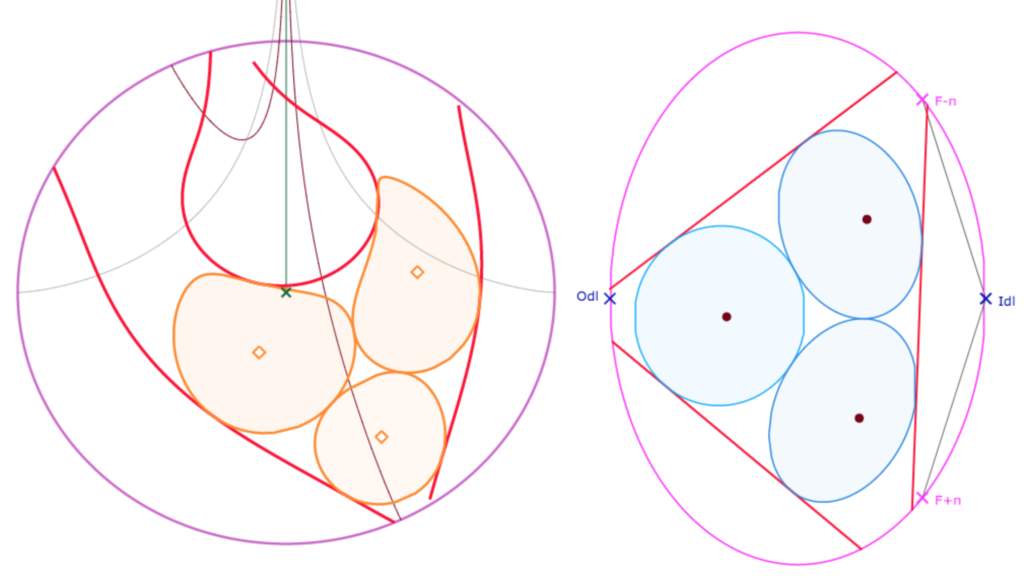
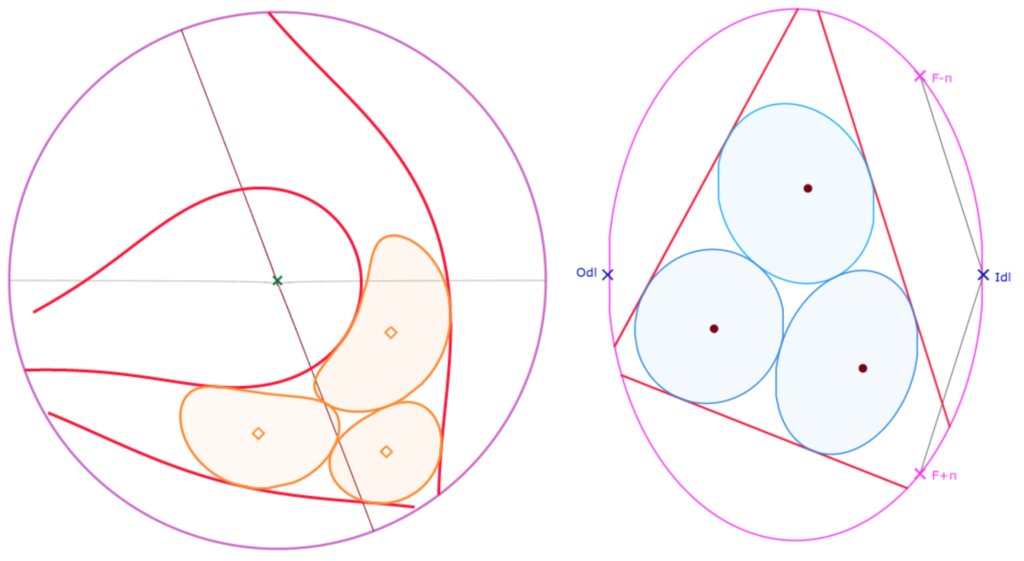
Mais aussi, dans une figure construite depuis KB, on peut observer des cercles de Malfatti multifeuilles
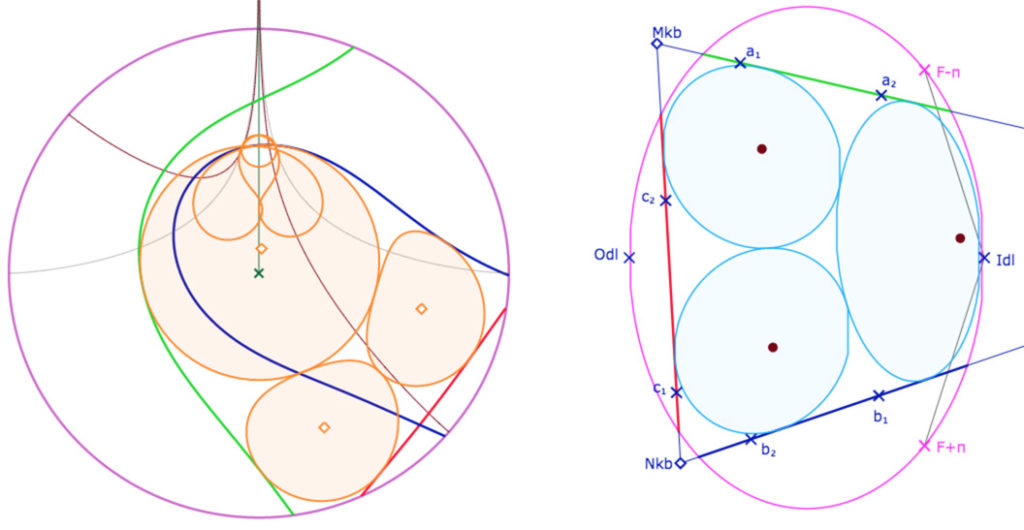
Deux figures sont présentées et manipulables dans cet article : une figure de conjugaison, avec les points de départ sur la pseudosphère, puis une figure de transfert d’une construction depuis le modèle de Klein-Beltrami comme ci-dessus.
La version KB de la construction de Malfatti est aussi utilisée pour illustrer un passage du Saggio de Beltrami (page suivante du menu) qui pourrait paraître un peu obscur en première lecture.
Compléments
Les macros utilisant la conjugaison
Pour réaliser soi-même des figures par conjugaison, consulter cet article qui propose plusieurs figures de départ avec de nombreuses macros … et leurs modes d’emploi.
Déploiement des feuilles adjacentes à la principale par changement de l’origine
Cet autre article propose des figures autour du changement d’origine de la PS dans KB. Cela permet de déployer les feuilles autour de la principale. C’est alors l’occasion de construire des cycles circonscrits de triangles – ci-dessous répartis sur 5 feuilles – « très enroulés » sur la surface, car proches de l’horicycle d’un côté (cercle – illustration 1) ou d’un autre (équidistante – illustration 2) comme on n’a pas l’habitude d’en croiser …
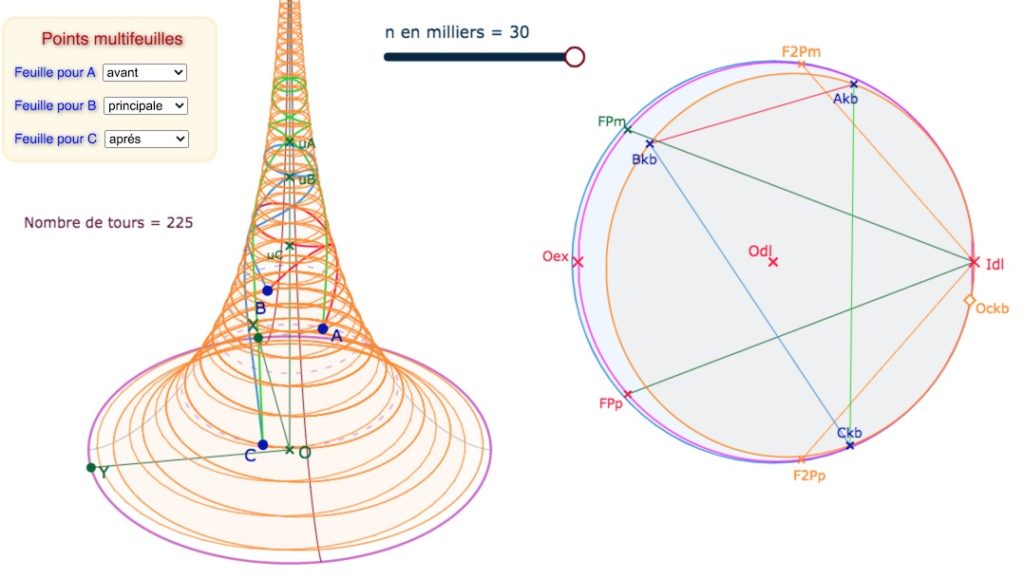
« n en milliers » est le nombre de segments du tracé du cycle, donc obtenu par programmation de listes de segments.