La question de la relation d’une géométrie plane métrique avec un plan projectif a, historiquement, deux approches. Tout d’abord celle de Cayley (1854) et de Klein (1869) qui consiste, étant donné le plan projectif, à regarder ce qui se passe à l’intérieur d’une conique. Ensuite est venue la démarche réciproque, initiée par Pasch mais surtout développée par Dehn (1900) qui consiste à partir d’une géométrie plane et à la compléter en un plan projectif par adjonction de points et de droites.
« Pour passer de la notion d’un espace limité à celle de l’espace projectif, il suffit d’adjoindre aux points qui composent l’espace limité de nouveaux éléments convenablement définis auxquels on a donné le nom de points idéaux. […] On les définit en généralisant le concept de « gerbes de droites » […] Lorsque les gerbes ne se rencontrent pas toutes en un même point de la région limitée de l’espace envisagé, on dira que la gerbe est impropre pour cette région et que ses droites ont en commun un point idéal. »
Principes de géométrie – Encyclopédie des sciences mathématiques.
Dans ces quelques pages, on aborde la question générale de ce plongement des plans métriques de Bachmann essentiellement d’un point de vue culturel, sans reprendre ses démonstrations, parfois longues ou fastidieuses. Il s’agit de proposer ici des illustrations dynamiques des notions mises en jeu, en particulier parce que la géométrie dynamique permet à la fois de rendre compte facilement des questions rencontrées mais aussi – sur le cas hyperbolique – d’explorer des résultats plus précis que ceux de la théorie générale, essentiellement à titre d’illustration et d’appropriation des concepts proposés.
Bachmann rappelle régulièrement que sa démarche s’inscrit dans une continuité historique : Tout d’abord, le premier modèle plan de la géométrie hyperbolique à l’intérieur d’un cercle (de Klein-Beltrami), totalement projectif, a été une source de représentation significative pour ce plongement : les symétries orthogonales hyperboliques étaient déjà les homologies harmoniques qui définissaient l’orthogonalité. Ensuite Dehn a effectivement opéré ce plongement pour le cas hyperbolique dans le cas réel (avec des distances). Le travail de Bachmann a été d’avoir su adapter, dans le contexte d’axiomatique absolue générale (et algébrique), les outils déjà mis en place par ses prédécesseurs, comme les demi-rotations de Hjelmslev auxquelles est consacrée cette page.
Pour cette partie, Bachmann distingue les pinceaux à centre des autres en nommant les premiers « pinceaux propres », et les autres (à axe ou sans support) « impropres ». Nous avons vu, lors de la séparation des géométries, que dans le cas elliptique tous les pinceaux sont propres. Ainsi le processus de plongement par les pinceaux comme points idéaux n’apporte rien en terme de nouveaux points. Et c’est inutile dans ce cas puisqu’un plan elliptique métrique est déjà un plan projectif métrique.
On pourrait donc se placer dans la suite, sans nuire à l’exhaustivité du procédé, dans une situation qui exclut le cas elliptique, plus précisément dans le cas où, par un point, il n’existe toujours qu’une seule perpendiculaire à une droite, puisque le cas elliptique est le seul qui ne vérifie pas cette condition. Ce n’est certes pas la démarche de Bachmann, au contraire, puisqu’il a cherché une généralisation « absolue » à la démarche initiale de Hjelmslev.
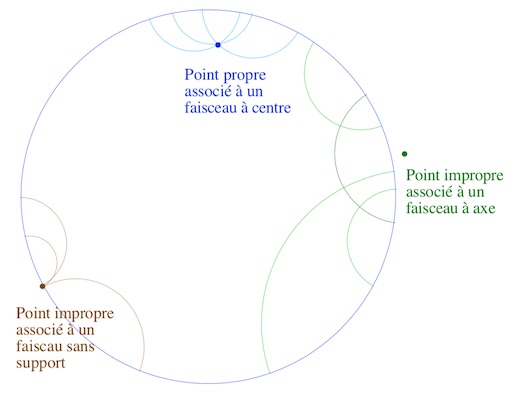
Les pinceaux étant les nouveaux points du plan projectif, il convient de les retrouver dans notre modèle DP. Les pinceaux propres correspondent aux points intérieurs au cercle. Les pinceaux à axe s’identifient au centre euclidien de l’axe qui peut être à l’infini dans n’importe quelle direction si l’axe est un diamètre du cercle, les pinceaux sans support sont identifiés aux points du cercle : on a déjà tous les points du plan idéal.
Il s’agit de construire les droites, puis la polarité. Pour illustrer la démarche de Bachmann, on se placera systématiquement dans le plan hyperbolique comme ci-dessus puisqu’on y dispose des trois types de pinceaux. Même si nous allons continuer à illustrer les principes de ce plongement dans le modèle du disque de Poincaré, pour dégager les idées générales de Hjelmslev et de Bachmann, plaçons nous un instant dans le modèle de Klein, plus intuitif pour le plongement projectif, puisque construit sur des arguments projectif : on a envie que les droites hyperboliques (cordes du disque KB) se prolongent en les droites usuelles du plan. Ce procédé naturel rendra compte de ce que Bachmann va appeler les droites idéales propres. La question est comment atteindre les autres ? Comment ramener, pour ce qui est de nos illustrations, les droites qui ne rencontrent pas le disque [du modèle] à partir de manipulations qui sont internes au plan hyperbolique ?
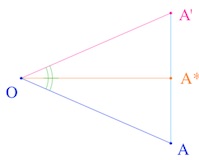
Bachmann propose l’illustration ci-contre (Aufbau p.91) comme situation fondamentale: \(A’\) est l’image de \(A\) dans une rotation de centre \(O\). Hjelmslev s’est alors intéressé au milieu \(A^*\) de \([AA’]\). Si \(O\) est, dans nos modèles (KB et DP), le centre de l’horizon, les symétries orthogonales sont, dans les deux cas, des symétries euclidiennes, et le passage de \(A\) à \(A^*\) est une similitude de rapport \(\displaystyle \frac{1}{cos \theta}\), si l’angle de la rotation est \(2\theta\). Et donc, si on sait donner un sens à cette transformation, d’un point de vue absolu, on voit que l’on pourra « ramener » toute(2) droite du plan sur une droite qui rencontre le cercle par un choix convenable de l’angle de la rotation (puisque la similitude est de rapport aussi petit que l’on veut) : une droite idéale sera alors l’image réciproque d’une droite idéale propre. Bien entendu ceci n’est qu’une représentation. Il n’y aura pas de similitude, ni d’angle ou de rapport. Mais cette représentation est suffisamment éclairante pour que Bachmann la propose pour illustrer ce passage de \(A\) à \(A^*\) que Hjelmslev a appelé demi-rotation.
(2) Sauf la droite de l’infini si \(O\) est le centre du cercle : dans les modèles, le centre de l’horizon a un rôle trop particulier. Pour éviter cette situation, on choisira \(O\) quelconque autre que le centre de l’horizon.
De même, le point de vue ponctuel illustré ci-dessus (approche de Hjelmselv), ne va pas convenir dans l’axiomatique de Bachmann dont les objets premiers sont les droites. Il va donc falloir l’adapter. L’organisation de cette partie est donc claire. Elle est rédigée sur deux pages (pour des manipulations plus fluides des figures) :
Cette page
- définir les demi-rotations, à partir de l’approche algébrique de Bachmann,
- étudier leur action sur les pinceaux en général (points du plan idéal),
Les pages suivantes
- définir les droites idéales du plan des pinceaux,
- étendre la notion de polarité naturelle aux droites idéales propres à l’ensemble des droites idéales,
- s’assurer que le plan idéal obtenu est bien un plan projectif métrique.
Les demi-rotations
Bachmann commence par algébriser le concept de demi-rotation de Hjelmslev. Le contexte général est celui de deux droites \(u\) et \(v\) non orthogonales et sécantes en un point \(O\), de sorte que \(uv \neq O\) (mais aussi \(uv \neq 1\)). Le point \(O\) peut être considéré comme fixe dans toute cette partie : le plongement se fait à partir d’un point origine donné, et on montre ensuite, à la fin, qu’il ne dépend pas de ce point.
Notations et définition
On notera \(H_{uv}\) une demi-rotation (\(H\) venant aussi bien de l’allemand Halb que de l’anglais Half).
On notera, comme usuellement, \(H_{uv}(g)\) ou \(H_{uv}(A)\) l’image d’une droite ou d’un point par une demi-rotation. En effet, la notation exponentielle correspond à une conjugaison dans l’ensemble des isométries du groupe de Bachmann. Ici \(H_{uv}\) n’est pas une isométrie, nous utilisons donc une autre notation, réservant l’exponentiation aux seules isométries.
Définition de l’image d’une droite par une demi-rotation
Préférer ouvrir cette figure dans un nouvel onglet.
Particularité du cas elliptique
Dans le cas d’une droite \(b\) non incidente à \(O\), on note plus généralement \(F\) le pied d’une perpendiculaire \(w\) à \(b\) issue de \(O\) (et non pas « de la »). Regardons ce qu’il en est dans le cas où \(b\) est la polaire de \(O\) (seul cas où \(F\) ne serait pas unique). Dans ce cas, toute droite \(w \mid b\) passe par \(O\) et donc \(H_{uv}(w) \mid b\). Ainsi, quelque soit le point \(F\) de \(b\) choisi, \(H_{uv}(b)=b\) : dans une demi-rotation de centre \(O\), la polaire de \(O\) a pour image elle-même. La définition de la demi-rotation dans ce cas ne dépend pas du point \(F\) retenu pour une perpendiculaire.
Une propriété immédiate
Avec cette définition, la droite image d’une droite \(d\), par une demi-rotation de centre \(O\), contient toujours le (les) pied(s) de la (des) perpendiculaire(s) à \(d\) issue(s) de \(O\). C’est immédiat mais cela servira pour l’image d’un pinceau par une demi-rotation.
Aspect demi-rotation
Notons \(h = H_{uv}(a)\), et \(a’=a^{uv}\), l’image par la rotation \(uv\) de la droite \(a\). Dans le cas d’une droite \(a\) du pinceau \(\mathscr{P}_{uv}\), \(h\) est aussi une droite du pinceau. Or \(a^h=hah=auv.a.auv=auvuv=vuauv=a^{uv}=a’\)(car \(auv = vua\) puisque c’est une droite). Ainsi, pour une droite \(a\) du pinceau à centre \(\mathscr{P}_{uv}\), l’image par la demi-rotation \(H_{uv}\) est bissectrice de \((a, a^{uv})\), d’où l’expression de demi-rotation.
Non bijection sur l’ensemble des droites
On vérifierait que \(H_{uv}\) est une injection de l’ensemble des droites du plan métrique dans lui- même. Mais ce n’est pas une bijection sur l’ensemble des droites comme on peut l’explorer dans la figure suivante.
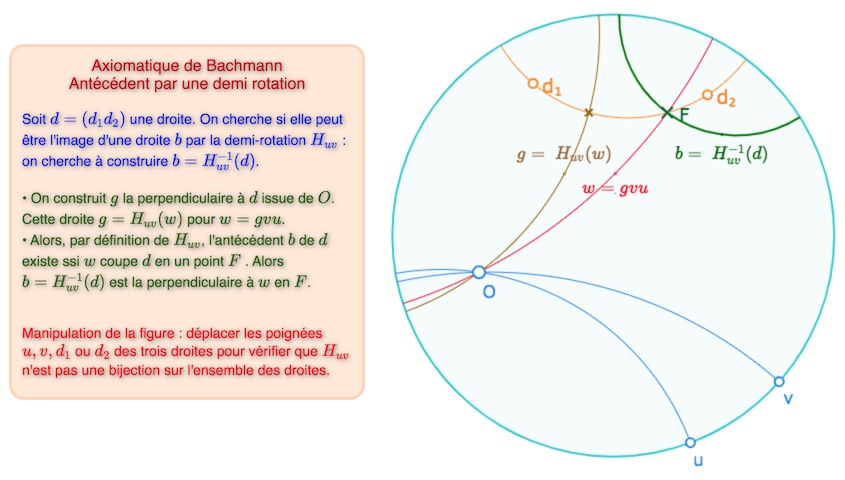
Lancer cette figure dans un nouvel onglet.
Caractérisation des droites ayant un antécédent par \(H_{uv}\)
On sort ici du travail de Bachmann pour poursuivre l’exploration dynamique élémentaire des demi-rotations dans le modèle du disque de Poincaré. On résume la situation dans les deux figures suivantes. Pour rappel, dans ce site, on a longuement détaillé les constructions hyperboliques (au sens de « absolues », hors modèle) de Janos Bolyaï, des fonctions notées \(\Pi\) et \(\Delta\) par Lobatchevsky, au début du second article consacré à son célèbre mémoire intitulé « La science absolue de l’espace ».
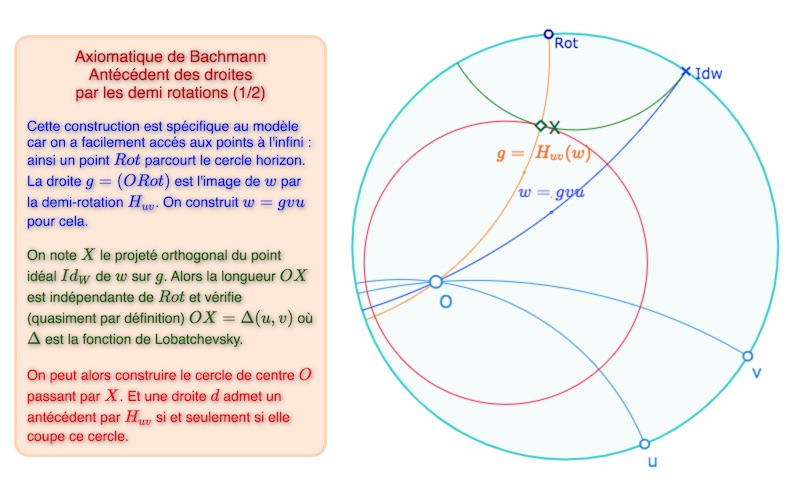
Éventuellement ouvrir cette figure dans un nouvel onglet (mais pas vraiment utile).
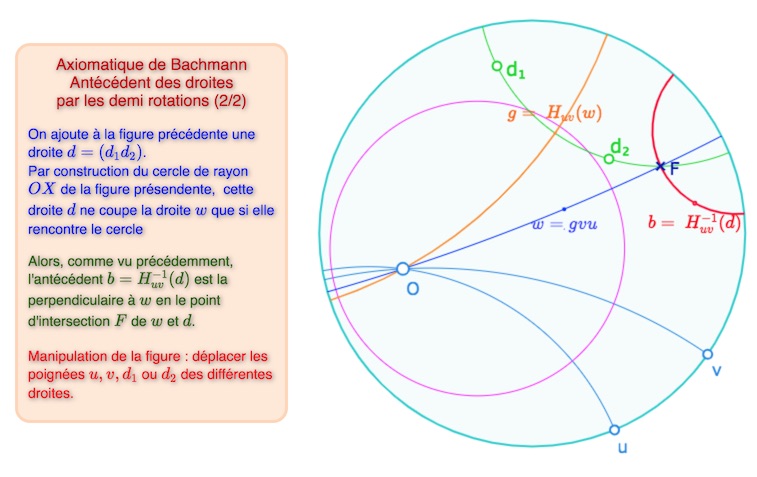
Ouvrir cette figure dans un nouvel onglet (plus intéressant bien entendu).
Dans la suite, on notera \(\mathscr{C}_{uv}\) le cercle de centre \(O\) de rayon \(\Delta(u,v)\), et \(\mathscr{D}_{uv}\) le disque associé. Le paragraphe suivant montre que c’est l’image – ponctuelle – du plan hyperbolique par \(H_{uv}\). On peut observer que le cercle serait de rayon nul pour \(u \perp v\) ce qui est exclu par hypothèse.
Image d’un point par \(H_{uv}\)
On reprend désormais le déroulé de Bachmann. Un point \(P\) étant défini comme le produit de deux droites orthogonales, on peut facilement construire l’image d’un point par une demi-rotation. L’image de \(O\) est \(O\). Pour tout point \(P\) autre que \(O\), \(P\) est l’intersection des droites \(a=(OP)\) et de sa perpendiculaire \(b\) en \(P\). L’image de \(P\) est l’intersection des droites images : elles se coupent car, dans ce cas précis(3) \(H_{uv}(b)\) est orthogonale à \(H_{uv}(a)\). On a vu que \(H_{uv}(a)\) est la bissectrice de \((a, a^{uv})\), \(H_{uv}(P)\) est la projection orthogonale de \(P\) sur \(H_{uv}(a)\), ou encore le(4) milieu de \(P\) et de \(P^{uv}\).
(3) D’une droite du pinceau \(\mathscr{P}_O\) – sinon les demi-rotations ne conservent en général pas l’orthogonalité. Hjelmslev a montré que les demi -otations conservent l’orthogonalité seulement dans le contexte euclidien.
(4) La « projection orthogonale » comme pied de perpendiculaire est unique, par contre le milieu pourrait ne pas l’être dans le cas elliptique (et ce n’est pas non plus le vocabulaire de Bachmann), mais cela l’est si on considère le milieu du segment elliptique \([PP^{uv}]\) et non pas seulement un des deux milieux des points \(P\) et de \(P^{uv}\).
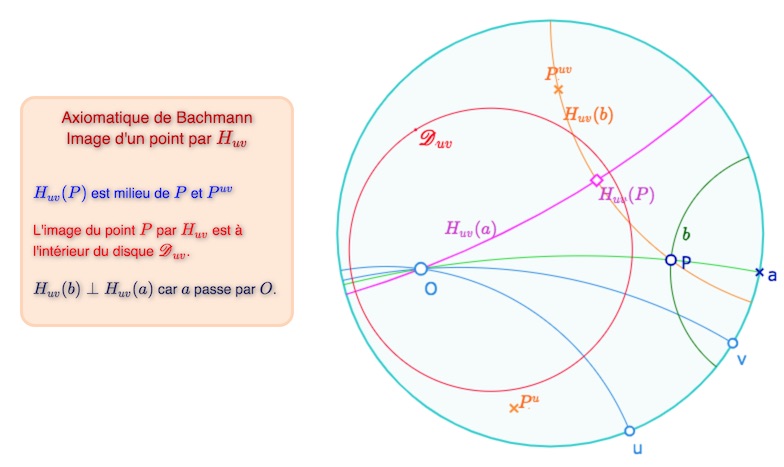
Lancer cette figure dans un nouvel onglet
Retour sur la question de l’incidence
Nous avions abordé, dans les pages d’introduction à l’axiomatique de Bachmann, cette question de la présentation séparée des points et des droites : les droites ne sont pas l’ensemble des points qui lui sont incidents. Outre qu’il s’agit d’une démarche théorique de fond, nous retrouvons ici une des illustrations de la nécessité de ce point de vue : pour une généralisation absolue des demi rotations de Hjelmslev, dont l’essentiel de l’utilisation va être l’action sur les pinceaux, il faut que ces transformations opèrent sur les droites indépendamment de l’incidence et des points.
Préférer ouvrir cette figure (un peu plus grande) dans un nouvel onglet
Compléments sur cette figure (propres au modèle utilisé bien entendu) : Les points limites sur le cercle \(\mathscr{D}_{uv}\) sont les images des points idéaux (au sens usuel du terme) de la droite \(a\) : \(Ida_1\) et \(Ida_2\). Les droites \((Ida_1Ida_1^{uv})\) et \((Ida_2Ida_2^{uv})\) sont les tangentes à \(\mathscr{D}_{uv}\) en ces points limites.
Autre construction de l’image d’une droite
Ce point de vue ponctuel va nous servir pour les constructions dynamiques, et en particulier cette propriété :
Propriété : l’image d’une droite \(b\) par la demi-rotation \(H_{uv}\) est la droite passant par les pieds \(Q\) et \(Q^{uv}\) des perpendiculaires à \(b\) et \(b^{uv}\) issues de \(O\).
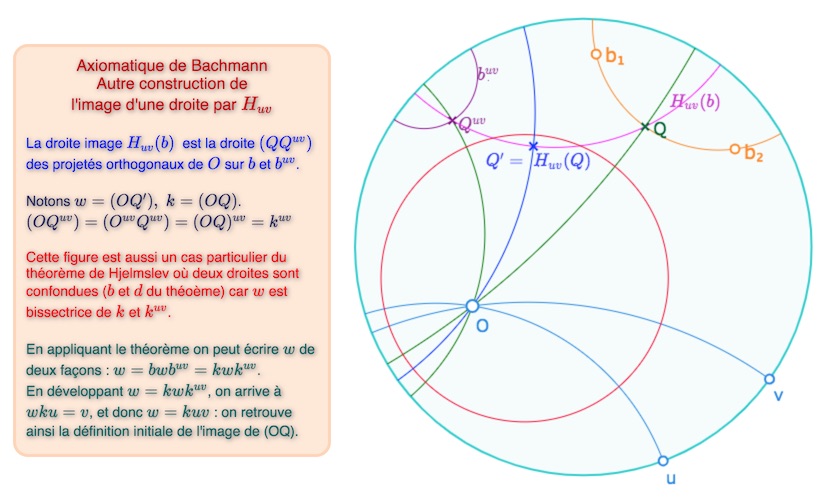
Ouvrir cette figure dans un nouvel onglet.
Revoir le théorème de Hjelmslev : c’est le théorème 12 de cette page.
Détail du calcul : en reprenant \(w=kwk^{uv}\), il vient \(v^{wku}=v\). Et donc la droite \(wku\) est soit orthogonale à \(v\) (et alors \(wkuv=O\)) soit \(wku=v\). La première option n’est pas possible, il reste \(wku=v\) soit \(w=kuv\), c’est-à-dire \((OQ’)=(OQ)uv\) : on retrouve la définition initiale de l’image d’une droite passant par \(O\).
Image des pinceaux par les demi-rotations
Les pinceaux étant au cœur de la construction du nouveau plan, l’effet des demi-rotations sur les pinceaux est une question essentielle (pour laquelle elles ont été inventées). La première propriété est que la notion de pinceau est conservée, et en particulier (par conservation de l’incidence, due à celle de l’alignement) les pinceaux propres sont conservés : l’image d’un pinceau à centre est un pinceau à centre. Pour les autres types de pinceau, explorons la situation sur une figure.
Exploration du contexte avec une figure générique
On considère le pinceau \(\mathscr{P}_{ab}\) défini par les droites \(a=(a_1a_2)\) et \(b=(b_1b_2)\). la troisième droite \(c\) est pilotée par la poignée \(c_1\). On construit \(H_{uv}(\mathscr{P}_{ab})\) avec des droites de même couleur, en utilisant la propriété précédente. Une droite et son image se coupent en la projection orthogonale de \(O\) sur le droite initiale : en \(A\) sur \(a\), en \(B\) sur \(b\) et en \(C\) sur \(c\).
Dans les illustrations suivantes, on s’intéresse au lieu (en rouge) du centre \(C_{im}\) du pinceau image quand cette mage est « à centre ».
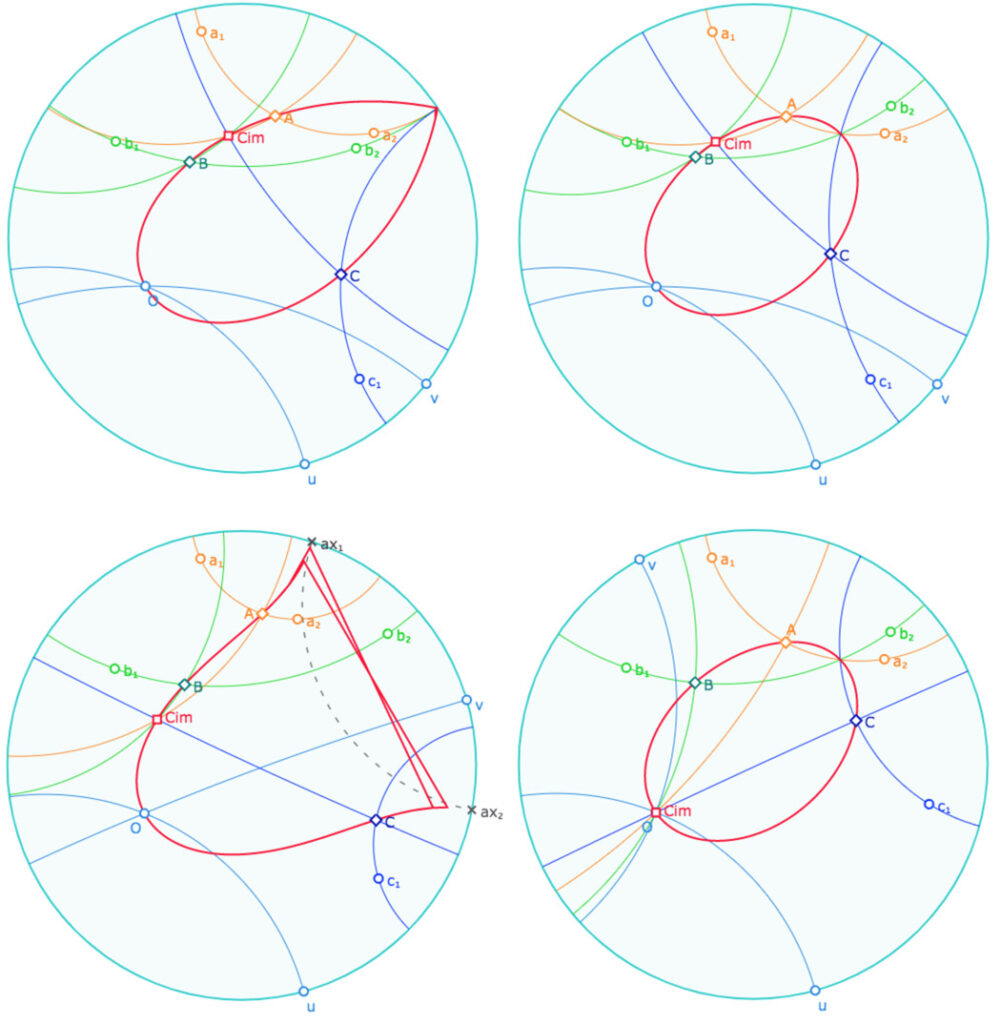
En haut à gauche : A L’ouverture de la figure, \(\mathscr{P}_{ab}\) est sans support. le lieu montre que son image est toujours à centre (sauf dans le cas où la demi-rotation est l’identité ce qui est exclu par hypothèse).
En haut à droite : le pinceau initial est à centre, le lieu fermé illustre que l’image d’un pinceau à centre est toujours à centre.
En bas à gauche : le pinceau initial est à axe. Très désolé pour l’artefact du lieu que je n’ai pas réussi à enlever quand le pinceau initial est à axe !
En bas à droite, quand \(u \perp v\), le centre du pinceau image est en \(O\). On rappelle que la situation est exclue par hypothèse (on aurait \(\mathscr{D}_{uv}\) réduit au point \(O\))
Déplacer quelques poignées de droite. La figure est plus fluide si on cache le lieu de \(C_{im}\).
Préférer ouvrir cette figure, en version plus grande, dans un nouvel onglet.
Les premiers théorèmes absolus de Bachmann sur les pinceaux
Bachmann montre deux résultats absolus sur les pinceaux, essentiels pour sa construction :
R1 – Si un pinceau est à axe dont l’axe \(d\) passe par le point \(O\), alors son image est aussi un pinceau à axe, d’axe \(H_{uv}(d)\).
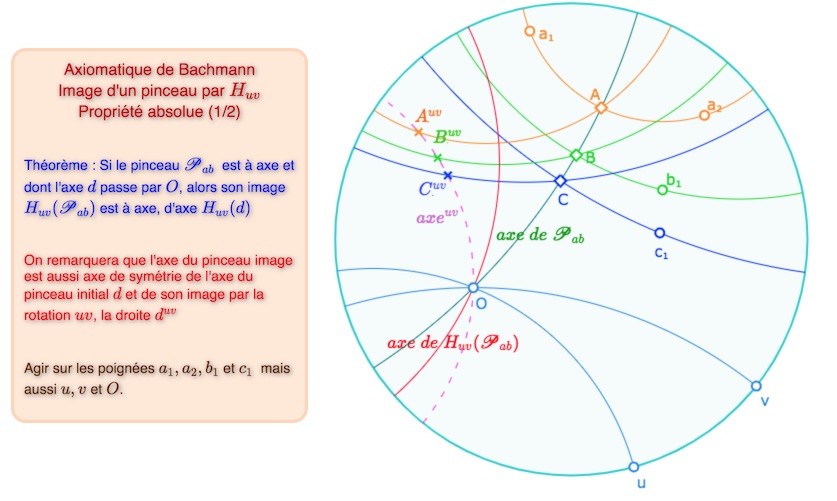
Illustration du premier théorème sur l’image d’un pinceau par une dem- rotation
Ouvrir la figure associée dans un nouvel onglet
Même si ce n’est pas abordé par Bachmann, on peut regarder l’autre cas hyperbolique de « pinceau impropre », le cas où le pinceau est sans support. On l’a déjà abordé avec la figure générique, mais voici une figure spécifique.

Ouvrir cette figure de pinceau sans support dans un nouvel onglet.
R2 – Pour tout autre pinceau impropre, il existe toujours une demi-rotation de centre \(O\) qui transforme ce pinceau en un pinceau à centre.
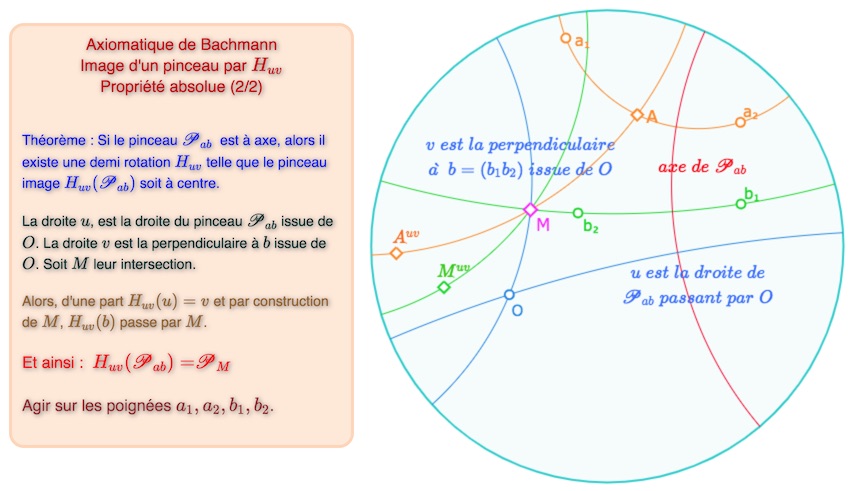
Construction proposée par Bachmann pour transformer un pinceau à axe en pinceau à centre
Ouvrir la figure associée dans un nouvel onglet.
La même construction fonctionne aussi pour un pinceau sans support (vrai de manière absolue, car il existe toujours une droite appartenant à un pinceau issue d’un point). Voici une illustration dans le cas « sans support » hyperbolique.
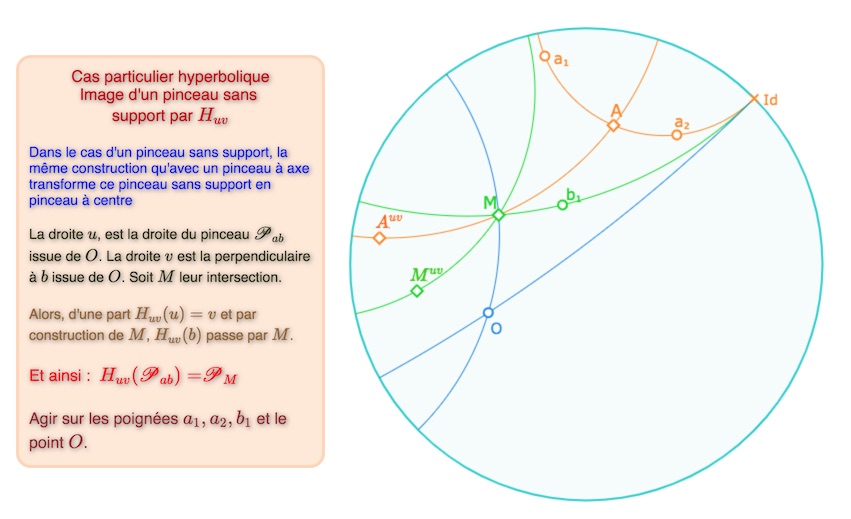
Ouvrir la figure associée dans un nouvel onglet.
Résumé de l’action des demi-rotations sur les pinceaux
Dans ce résumé, on notera les pinceaux non pas par leurs droites, \(\mathscr{P}_{ab}\), comme précédemment, mais par leur type : pour un pinceau d’axe \(d\), on écrira \(\mathscr{P}_d\), et comme d’habitude, \(\mathscr{P}_A\) pour un pinceau de centre \(A\), .
• L’image d’un pinceau à centre est un pinceau à centre : \(H_{uv}(\mathscr{P}_{A})=\mathscr{P}_{H_{uv}(A)}\).
• L’image d’un pinceau à axe \(d\) peut être à centre ou à axe.
– En général, même si l’image est un pinceau à axe, \(H_{uv}(\mathscr{P}_{d}) \neq\mathscr{P}_{H_{uv}(d)}\).
– si \(O \in d\), \(H_{uv}(\mathscr{P}_{d})\) est un pinceau à axe \(\delta\) : \(H_{uv}(\mathscr{P}_{d})=\mathscr{P}_{\delta}\) et \(O \in \delta\).
– si \(O \notin d, \exists uv, \exists M \; / \; H_{uv}(\mathscr{P}_{d})=\mathscr{P}_{M}\).