Il convient d’avoir lu la page précédente pour le détail des notions autour de la relation \( \mid \) d’orthogonalité et d’incidence.
On considère un groupe \(\Gamma\), noté multiplicativement, d’unité 1, engendré par un ensemble \(\Delta\) de générateurs, tous d’ordre 2, \(\Delta\) étant stable par conjugaison.
Les éléments de \(\Gamma\) sont généralement désignés par des lettres grecques, ceux de \(\Delta\) par des lettres minuscules latines. Une lettre majuscule latine désignera toujours le produit de deux générateurs quand ce produit est d’ordre 2 : on écrira \(P=ab \; (=ba)\) si \(a \mid b\) (et donc \(a \neq b\)). \(P\) est donc lui aussi un élément d’ordre 2 de \(\Gamma\).
Les axiomes et le vocabulaire associé
Axiomes d’incidence
A1. Pour tout \(P\) et \(Q\), il existe \(g\) tel que \(P, Q \mid g\).
A2. Si \(P, Q \mid g,h\), alors, soit \(P=Q\), soit \(g=h\).
Axiomes de tri-réflexions
A3. Si \(a, b, c \mid P\) alors il existe \(d\) tel que \(abc=d\).
A4. Si \(a, b, c \mid g\) alors il existe \(d\) tel que \(abc=d\).
Axiome d’existence
A5. Il existe \(g, h, j\) tel que \(g \mid h\) mais tel que l’on n’ait ni \(j \mid g\) ni \(j \mid h\) ni \(gh \mid j\).
Compte tenu de ce que l’on a vu à la page précédente, il est facile d’interpréter ces axiomes dans la géométrie euclidienne plane : ils n’en sont qu’une formalisation, qu’une « seconde axiomatisation » au sens de Gonseth. On notera toutefois que le groupe \(\Gamma\), même si on peut par exemple décider d’appeler ses éléments des isométries, n’est pas un groupe d’isométries d’un ensemble de points extérieurs. Nous sommes sur un groupe abstrait.
Certains auteurs(*) appellent « géométrie de Bachmann » la donnée du couple \( (\Gamma, \Delta)\) muni des 4 premiers axiomes, et réservent le nom de « géométrie absolue » la donnée du couple muni des 5 axiomes. Le cinquième axiome assure l’existence d’un vrai triangle rectangle (en \(gh\)). Cet axiome permettra de montrer qu’une droite a nécessairement au moins trois points distincts et en particulier on peut construire des « géométries de Bachmann » trop pauvres (droites à deux points) pour pouvoir être des « plans métriques ».
(*) Par exemple Michael Henle dans « Modern Geometry – the analytic approach » Prentice Hall 1997 (p. 327)
Exemple d’une géométrie de Bachmann qui n’est pas un plan métrique de Bachmann
\(\Gamma\) est le groupe de Klein (table ci-contre). On a \(a^2=b^2=c^2=1\) et \(ab=ba=c\)
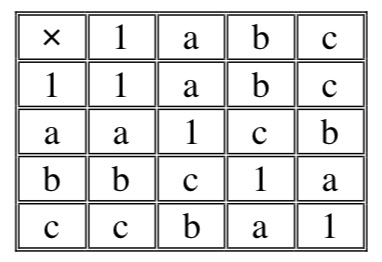
Il est engendré par \(\Delta=\{a,b,c\}\) et est stable par conjugaison. Bien entendu le groupe en engendré seulement par \(a\) et \(b\), mais si on veut que \(c\) soit une droite, il faut l’ajouter à \(\Delta\), ce qui montre que, dans la théorie, \(\Delta\) n’est pas nécessairement un système de générateurs minimal au sens de l’inclusion. Le couple \((\Gamma, \Delta)\) remplit bien les premières conditions pour être un groupe de Bachmann. On a tout de suite \(ab=c=C, \; bc=a=A\) et \(ac=b=B\). Au sens de Bachmann il y a donc 3 droites et trois points, qui sont tripolaires (chaque droite est un point).
Le premier axiome d’incidence est vérifié : si on prend deux points \(M\) et \(N\), il existe une droite \(g\) telle que \(M, N \mid g\) en effet \(M\) et \(N\) sont aussi deux droites et la troisième vérifie bien la relation \(\mid\) avec les deux autres. Le second axiome d’incidence est vérifié car sa prémisse \(P, Q \mid a, b\) ne peut pas être vérifiée : il n’y a pas assez de droites et de points (puisque | signifie que les objets ne sont pas de produit égal à 1).
Pour la même raison, les prémisses des axiomes de tri-réflexions ne sont jamais vérifiées donc les axiomes sont, eux, vérifiés : le groupe de Klein avec son ensemble de générateur vérifie bien les 4 premiers axiomes de Bachmann. Mais il ne vérifie pas le cinquième, car il y a bien un triangle rectangle, mais, il est tri-rectangle et donc ne vérifie pas l’axiome A5 du « vrai » triangle rectangle.
Cette géométrie minimale – non considérée comme plan métrique par Bachmann – correspond à une géométrie elliptique minimale: il n’existe qu’une figure, le triangle tripolaire.
Bachmann appelle, lui, « groupes de transformations » (« groups of motions » dans ses écrits anglo-saxons) les modèles de son système d’axiome et insiste bien sur le fait que ce système d’axiome n’a pas de signification pour un groupe \(\Gamma\) seul mais devient signifiant – ie n’est susceptible d’interprétations et de modèles – que si nous considérons le couple \( (\Gamma, \Delta)\). Comme on l’a vu ci-dessus, même si c’est un cas très particulier, l’ensemble des générateurs \(\Delta\) n’a pas à être minimal pour les propriétés voulues. Mais les géométries obtenues peuvent être différentes. Bachmann en donne des exemples.
Plan du groupe, pôle et polaire
Il s’agit ensuite de fixer un vocabulaire géométrique pour décrire les concepts algébriques mis en jeu dans ce système d’axiome. Pour ce faire, Bachmann donne au couple \( (\Gamma, \Delta)\) une dimension géométrique qu’il appelle le plan du groupe, en précisant désormais :
Les éléments de \(\Delta\) sont appelés les droites du plan. Les involutions de \(\Gamma\) qui peuvent s’exprimer comme produit de deux éléments de \(\Gamma\) sont les points du plan du groupe.
Deux droites \(a\) et \(b\) sont dites orthogonales, et on note \(a \perp b\) ssi \(a \mid b\). Ainsi, les points sont les éléments du groupe qui s’expriment comme le produit de deux droites orthogonales.
On dira également qu’un point \(P\) est incident à une droite \(g\) quand \(P \mid g\). L’incidence se note aussi \(P \, \mathfrak{I} \, g\) ou \(g \, \mathfrak{I} \, P\). On utilisera aussi le vocabulaire traditionnel d’incidence.
On remarquera que selon la règle retenue pour la relation \(\mid\), on ne parle pas d’incidence si \(P = g\) (car alors on aurait \(Pg=1\)).
Cette situation est à prendre en compte car elle n’est pas exclue par le système d’axiome. Si par exemple trois droites \(a, b, c\) vérifient \(abc=1\), alors on a \(ab=c\). Donc \(ab\) est d’ordre 2, c’est un point \(C\) qui vérifie \(C=c\). On est dans la situation où, dans le plan du groupe de Bachmann, un point est aussi une droite. Comme cette situation est possible dans son système d’axiome(*), et qu’il va falloir en tenir compte dans les démonstrations, il convient de préciser le vocabulaire suivant : si \(C=c\) le point et la droite sont dits en polarité, le point est appelé le pôle de la droite et celle-ci la polaire du point.
(*) C’est l’intérêt de cette axiomatique de ne pas exclure ce cas, c’est-à-dire d’inclure la possibilité elliptique. Bien entendu, cette possibilité a un coût : celui de devoir traiter régulièrement, dans les preuves, ce cas de polarité, avec l’avantage de montrer des théorèmes de géométrie « absolus » en un sens bien plus large que celui de Bolyai.
Nous voyons ici, à nouveau, un effet fort puissant. Clairement pour Bachmann, les éléments de sa géométrie étant ceux d’un groupe, droites et points sont d’abord des transformations, et c’est comme telles que l’on peut écrire \(C=c\) : la symétrie orthogonale d’axe \(c\) est égale à la symétrie centrale de centre \(C\). Mais, si on se réfère au chapitre ELL, avec le modèle euclidien de la géométrie elliptique, il est clair que dans aucune représentation plane géométriquement manipulable, on aura, concrètement, que le pôle d’une droite est « égal » à la droite, l’égalité, prise implicitement dans le champ des configurations, est celle d’ensembles, et non celle de l’action d’un élément d’un groupe sur ce groupe.
Retour temporaire à la première axiomatisation
Cette différence entre une axiomatisation aussi conceptuellement approfondie et la manipulation concrète des objets peut poser question, en particulier sur des représentations dans lesquelles l’incidence usuelle est respectée, c’est-à-dire où une droite est un ensemble de points, ce qui n’est pas le cas ici.
On peut y revenir – d’une certaine façon revenir au premier niveau d’axiomatisation – en proposant de définir le plan associé au couple \( (\Gamma, \Delta)\) de manière plus géométrique que Bachmann lui-même. Le plan est un sous-ensemble \(\mathscr{P}\) de \(\Gamma\) dont les éléments sont des points : ce sont toujours les produits latex]P[/latex] d’éléments de \(\Delta\) quand ce produit est d’ordre 2.
On définit alors les droites comme des parties de \(\mathscr{P}\) (ce qui n’est pas le cas dans Bachmann) qui vont être canoniquement en bijection avec \(\Delta\) : la droite \(\hat{a}\) associée à l’élément \(a\) de \(\Delta\) est l’ensemble: \(\hat{a}=\{ P \in \mathscr{P} \; / \; Pa\) est d’ordre 2 dans \(\Gamma \}\).
On a bien \(M \in \hat{a} \Longleftrightarrow M \mid a\), soit \(M\) incident à \(a\) au sens de Bachmann. De ce point de vue l’orthogonalité des droites se définit par \(\hat{a} \perp \hat{b} \Longleftrightarrow ab\) est d’ordre 2. La seule différence avec le plan du groupe de Bachmann est qu’une droite est une partie de \(\mathscr{P}\) (en bijection avec \(\Delta\)) au lieu d’en être un élément, et l’incidence est (re)devenue l’appartenance au sens usuel des ensembles. En ce sens, une droite n’est jamais égale à un point, ce qui correspond bien aux représentations que l’on se fait en manipulant le modèle elliptique du menu ELL : dans le champ des configurations, une droite elliptique ne peut pas s’identifier à son pôle, et si on a bien la possibilité d’avoir \(C=c\), on n’a pas \(C=\hat{c}\) et alors le pôle et sa polaire sont deux objets différents. Dans ce contexte, les notions de pôle et polaire peuvent se définir ainsi :
Soient \(P\) un point de \(\mathscr{P}\) et \(\delta\) une droite de \(\mathscr{P}\). On dit que \(\delta\) est la polaire de \(P\) (ou que \(P\) est le pôle de \(\delta\)) si l’une des deux conditions équivalentes suivantes est vérifiée :
\(\quad i) \; P \in \Delta\) et \(\delta = \hat{P}\).
\(\quad ii) \;\) Toute droite passant par \(P\) est orthogonale à \(\delta\).
Cette équivalence sera un corollaire du Théorème 2 montré plus loin.
Ce passage étant réalisé entre les deux niveaux d’axiomatisation, dans la suite, nous avons fait le choix de continuer de présenter l’axiomatique de Bachmann dans sa forme originelle, c’est-à-dire du côté de la seconde axiomatisation, aussi bien par respect pour le travail de son auteur, que pour le bonheur de présenter son élégance algébrique.
Droites en pinceaux et pinceaux de droites
Les axiomes structurant de ce système étant ceux dits de tri-réflexions, il est clair que les notions qui leur sont associées vont être au cœur de l’argumentation. Bachmann introduit à ce sujet une relation et un objet :
Trois droites \(a, b, c\) seront dites en pinceau si le produit \(abc\) est une droite.
Cette relation « être en pinceau » est symétrique : elle est indépendante de l’ordre dans lequel sont composées les droites. En effet, si \(abc\) est une droite, alors : \(cba=(abc)^{-1}\) est une droite. \(bca = a(abc)a = a(abc)a^{-1}\) aussi par stabilité par conjugaison. De même pour les trois autres relations : \(bac = c(cba)c\), \(acb = b(bac)b\) et \(cab = b(bca)b\).
Comme l’indépendance de l’ordre est fortement liée à la conjugaison, on pourrait penser que peut-être il y a là une version algébrique d’une utilisation cachée de l’ordre. Il n’en est rien : l’axiomatique de Bachmann est vérifiée sur de nombreux corps non ordonnables : sur les corps finis (et Bachmann montre qu’alors son axiomatique ne produit que des plans euclidiens finis, mais aussi sur des géométries plus conséquentes comme des plans sur \(\mathbb{Q(i)}\). Nous y reviendrons dans les pages traitant de la séparation des géométries et des corps associés, pour discuter du vocabulaire de Bachmann.
La possibilité d’arriver à une axiomatique qui n’utilise pas l’ordre est un point particulièrement travaillé par Bachmann. La relation est aussi, trivialement, réflexive, c’est-à-dire vérifiée dès que deux (au moins) des trois droites sont confondues. La question de la transitivité est essentielle ; elle est abordée à la page suivante.
À côté de cette relation, on introduit en même temps la notion de pinceau, comme objet : pour deux droites distinctes \(a \neq b\), l’ensemble des droites qui sont en pinceau avec \(a\) et \(b\) est appelé le pinceau de droites \(\mathscr{P}_{ab}\) ainsi noté car il ne dépend en fait que du produit \(ab\).
Les axiomes de tri-réflexions permettent de définir et d’étudier des pinceaux à centre (axiome 3) et à axe (axiome 4), mais la relation est assez souple pour s’appliquer à d’autres objets, et, dès son introduction, Bachmann mentionne – pour nous donner des représentations – la possibilité pour des pinceaux d’être d’un autre type, en particulier le pinceau des droites orthogonales à un horicycle dans le cas hyperbolique : le support sera le point idéal centre de l’horicycle. L’élégance de l’axiomatique de Bachmann se trouve à de nombreux endroits, et en particulier ici : la possibilité d’étudier, grâce à la relation « être en pinceau », d’autres types de pinceaux que ceux implicitement mentionnés dans les axiomes. Bachmann les appelle pinceaux « sans support ».
Avec un peu de pratique – en seconde lecture – une question vient nécessairement sur ce troisième type de pinceau : est-ce vraiment un type de pinceau (comme dans le cas hyperbolique), ou bien cette expression englobe-t-elle tout ce qui n’est pas connectable (intersection des droites sur la conique associée, nous sommes en seconde lecture), et dans ce cas, peut-il y avoir plusieurs types différents de pinceaux « sans support » ? Nous reviendrons sur cette question quand nous aborderons la séparation des géométries.
Collinéations
Avant d’aborder les premières conséquences élémentaires des axiomes, voyons maintenant la définition de deux collinéations du plan du groupe de Bachmann. Une collinéation est une application qui conserve les ensembles de droites, de point, et l’incidence. Elle est dite orthogonale si de plus elle conserve aussi l’orthogonalité.
Soit \(\alpha \in \Gamma\), considérons la transformation \(T_{\alpha}\) définie sur \(\Gamma\) par \(T_{\alpha}(\gamma) = \gamma^\alpha\). Comme \(\Delta\) est stable par conjugaison, l’image d’une droite est bien une droite. De plus, si on note \(P=gh\) avec \(g \mid h\), on a, par les propriétés propres à la conjugaison, \(P^{\alpha}=g^{\alpha}h^{\alpha}\) avec \(g^{\alpha} \mid h^{\alpha}\), ainsi l’image d’un point par \(T_{\alpha}\) est un point, et cette transformation conserve aussi bien l’incidence que l’orthogonalité : c’est donc une collinéation orthogonale.
On peut appeler cette transformation \(T_{\alpha}\) une isométrie du plan et en particulier pour \(\alpha = a\) on parlera de réflexion (symétrie orthogonale) d’axe \(a\) et pour \(\alpha = A\) de réflexion (symétrie centrale) de centre \(A\) du plan (du groupe).
Le terme axe est repris pour droite par tradition géométrique ; il n’y a aucune connotation d’orientation dans le mot axe . Bachmann utilise droite. Il n’emploie jamais d’expression qui pourrait évoquer, même de loin, une référence à un ordre.
Regardons les droites invariantes par une réflexion orthogonale d’axe \(u\), on cherche les droites \(a\) telles que \(a^u=a\). C’est bien sûr vrai pour \(a=u\), sinon il faut \(uau=a\) soit \(u \mid a\).
Autrement dit les seules droites (globalement) invariantes par une symétrie orthogonale sont la droite de la symétrie et ses perpendiculaires.
Qu’en est-il des points ? \(A^u=A\) est équivalent à \(Au=uA\) soit \(A \mid u\) si \(A \neq u\) soit \(A=u\) : les seuls points invariants par une symétrie orthogonale sont les points incidents à la droite qui définit la symétrie ou le pôle de la droite … si ce pôle existe.
Tant que nous n’aurons pas séparé les géométries, nous serons amenés à traiter systématiquement cette question du pôle. Ce sera toujours sous réserve d’être dans une structure où il existe. En fait, quand nous aborderons la question, nous montrerons que toute droite a un pôle dès qu’une droite en a un : ce sera la géométrie elliptique.
De même les seules droites globalement invariantes par une symétrie centrale sont les droites passant par le centre ou la polaire du centre. Pour les poins invariants, il faut un minimum de propriétés sur l’orthogonalité : le résultat que chacun imagine sera montré après les premiers théorèmes.
Enfin, les mêmes propriétés de la conjugaison assurent que l’image de « trois droites en pinceau » par une isométrie \(T_{\alpha}\) est « trois droites en pinceau », c’est donc en particulier vrai pour les réflexions.
Conséquences des axiomes sur l’incidence et l’orthogonalité
(les 5 premiers théorèmes de l’exposé de Bachmann)
La rédaction d’un système d’axiomes est traditionnellement minimaliste. Nous voulons dire par là qu’ils contiennent en eux même plus que leur propre expression, sous forme de conséquences immédiates ou de réciproques que l’on peut tout de suite préciser. C’est l’objet de cette section et de la suivante. Dans cette section, on utilise essentiellement la relation \(\mid\) qui traite aussi bien de l’incidence d’un point et d’une droite que de l’orthogonalité de deux droites. Rappelons que, d’une manière générale, pour tout élément de \(\Gamma\), quand nous écrivons la relation \(\alpha \mid \beta\), cela contient toujours que \(\alpha \neq \beta\).
Avant d’aborder ces premiers développements, dans son exposé Bachmann commence par rendre compte des modèles usuels réels (elliptiques, euclidiens, et hyperboliques) au regard de son axiomatique. Seules les propriétés relatives à la stabilité des générateurs par conjugaison et celles décrites par les axiomes de tri-réflexions sont à vérifier. Elles relèvent dans les modèles de Poincaré et le modèle plan elliptique, des propriétés de l’inversion et dans le modèle projectif de Klein-Beltrami, de propriétés de l’homologie harmonique.
Th 1 : indépendance d’un point des droites qui le définissent
\((a, b) \mid P \; et \; (a \perp b) \Longleftrightarrow (P=ab)\)Soient deux droites distinctes \(a\) et \(b\), telles que \(P \mid a,b\) et \(a \mid b\) alors \(P=ab\) et réciproquement.
Sens direct
\(ab\) est un point \(Q\) tel que \(Q \mid a, b\) car \(aQ=b\) est d’ordre 2 et \(Qb=a\) aussi d’ordre 2. On a donc \(P, Q \mid a, b\) avec \(a \neq b\). Donc par l’axiome A2, il en résulte que \(P=Q\).
Sens réciproque
Si \(P=ab\), alors \(a \mid b\) et \(aP=b\) est d’ordre 2, donc \(P \mid a\). De même \(Pb=a\) est d’ordre 2, donc \(P \mid b\).
Th 2 : triangle trirectangle et produit de droites unitaire
\(abc=1 \Longleftrightarrow (a \mid b \; \mathrm{et} \; b \mid c \; \mathrm{et} \; c \mid a)\)Il y a équivalence entre l’orthogonalité de trois droites prises deux à deux et le produit des trois égal à 1.
Le sens direct (immédiat) a été abordé dans une page précédente, avec la présentation des notations.
Réciproquement, si les droites sont deux à deux orthogonales, on a \( (ab)^2=1, \; (bc)^2=1, \; (ca)^2=1,\). Il en résulte que \( (abc)^2=1\). Et donc, soit \(abc=1\), soit \(abc \neq 1\). On se place dans la seconde alternative pour montrer une contradiction. Notons \(C=ab\). \(C\) est un point car \(a \mid b\)., et de plus \(C\) n’est pas égal à \(c\) – ou encore n’est pas le pôle de \(c\), car, justement, nous somme dans l’hypothèse où \(abc\) est différent de 1. Mais de \( (abc)^2=1\) (involutive) en en déduit que \( ab \mid c\). Et donc \(C \, \mathfrak{I} \, c\) (car \(C\) n’est pas égal à \(c\)). Par ailleurs \(C=ab \mid b\) donc \(C\) est aussi incident à \(b\).
Nous sommes donc dans la situation où \(C\) est incident à la fois à \(b\) et à \(c\), avec \(b \mid c\) (les droites sont orthogonales). D’après le théorème 1, alors \(C=bc\). Autrement dit \(ab=bc\), soit \(a=c\), ce qui est contradictoire avec le fait que les droites \(a\) et \(c\) soient orthogonales : \(a \mid c\).
Figure associée à ce Th 2 (déjà présentée ici)
Avec la notation standard, on a \(N=s_{(AB)}(M)=s_c(M)\), \(P=s_{(AC)}(N)=s_b(N)=s_b o s_c(M)\) et \(Q=s_{(BC)}(P)=s_a(P)=s_a o s_b o s_c(M)\).
Alors \(Q=M\), soit \(s_a o s_b o s_c = Id\).
On peut déplacer les points \(A, B\) et \(M\).
Commentaire pour les lecteurs ayant déjà pratiqué la géométrie elliptique : Dans cette figure, observer qu’on peut placer le point \(M\) tel que les segments passent par les pôles des droites et donc que le triangle des milieux \(ABC\) est tripolaire alors que ce n’est pas le cas du triangle initial \(MNP\).
Retour à la caractérisation de la polarité dans la version dite « de première axiomatisation »
\(P\) est un point et \(\delta\) une droite de \(\mathscr{P}\) sous ensemble de \(\Delta\). Nous avions dit que \(\delta\) est la polaire de \(P\) si l’une des conditions suivantes (équivalentes) est vérifiée :
\( (P \in \Delta \; \mathrm{et} \; \delta = \hat{P}) \quad \Longleftrightarrow \quad\) (Toute droite passant par \(P\) est orthogonale à \(\delta\)).
Sens direct
Soit \(\hat{a}\) une droite passant par \(P\). Cela signifie que \(Pa\) est d’ordre 2 et donc que \(\hat{a}\) est orthogonale à \(\hat{P}=\delta\).
Sens réciproque
Posons \(\hat{d}=\delta\) et soient \(b\) et \(c\) de \(\Delta\) telles que \(P=bc\). Comme le produit \(bc\) est d’ordre 2 cela signifie que \(\hat{b}\) et \(\hat{c}\) sont orthogonales. Et comme elles passent toutes les deux par \(P\) elles sont, par hypothèse, orthogonales à \(\hat{d}\). D’après le théorème 2 (sens réciproque) on a donc le produit \(bcd=1\) et comme \(P=bc\), on a bien \(P=\hat{d}=\delta\).
Th 3 : existence de perpendiculaires
Pour \(P\) et \(g\) donnés, il existe \(h\) tel que \(P, g \mid h\)
Par un point il passe (au moins) une perpendiculaire à une droite donnée incidente à ce point.
Pour montrer ce théorème on distingue deux cas selon que \(P\) est – ou non – incident à la droite \(g\).
Cas 1 : \(P\) est incident à \(g\)
On a donc \(P \mid g\). Alors \(Pg\) est une droite. En effet, en notant \(P=ab\), par le sens direct du théorème 1, il vient \(g, a, b \mid P\). Et par l’axiome A3, il existe une droite \(h\) telle que \(abg=h\), soit \(Pg=h\). On a donc aussi \(P=hg\) et donc, par la réciproque du théorème 1, on a à la fois \(P \mid h\) et \(h \mid g\) : la droite \(h\) est orthogonale à \(g\) et incidente à \(P\).
Ce résultat (avec son unicité) sera un des axiomes de la version « géométrique » de l’axiomatique de Bachmann comme nous le verrons plus loin.
Illustrations de ce cas 1 dans le contexte le plus général : la situation elliptique
Dans la figure proposée en fin de démonstration, on considère une droite \(g\), pilotée par deux poignées, les points \(g_1\) et \(g_2\), et un point \(P\). On note \(G\) le pôle de \(g\). Dans le cas ou \(P \mid g\), on se donne deux droites \(a\) et \(b\), la première , orange, pilotée par le point \(a\)(poignée de la droite), telles que \(P=ab\), et donc \(b\), la droite verte, est orthogonale à \(a\) en \(P\). La droite rouge est la droite \(h=gab\). Si le théorème assure l’existence de cette droite, elle ne donne aucun moyen pour la construire. Pour cela il faudra attendre le théorème fondamental de Hjelmlev qui sera présenté dans une prochaine page.
Dans l’illustration suivante, (cas \(P\) incident à \(g\) donc) on prend un point \(M\) sur la droite \(a\) et on note \(Mg\) (pour \(M^g\)) son symétrique par rapport à \(g\), puis \(Mga\), le symétrique de \(Mg\) par rapport à \(a\) et enfin \(Mgab\) son symétrique par rapport à \(b\). La droite rouge, la droite \(gab\) est construite comme une des médiatrices de \(M\) et \(Mgab\). L’illustration est aussi l’occasion re rappeler quelques propriétés elliptiques, en particulier sur les segments et les symétriques. On peut se reporter à cette page sur la symétrie elliptique et celle-ci sur les segments elliptiques.
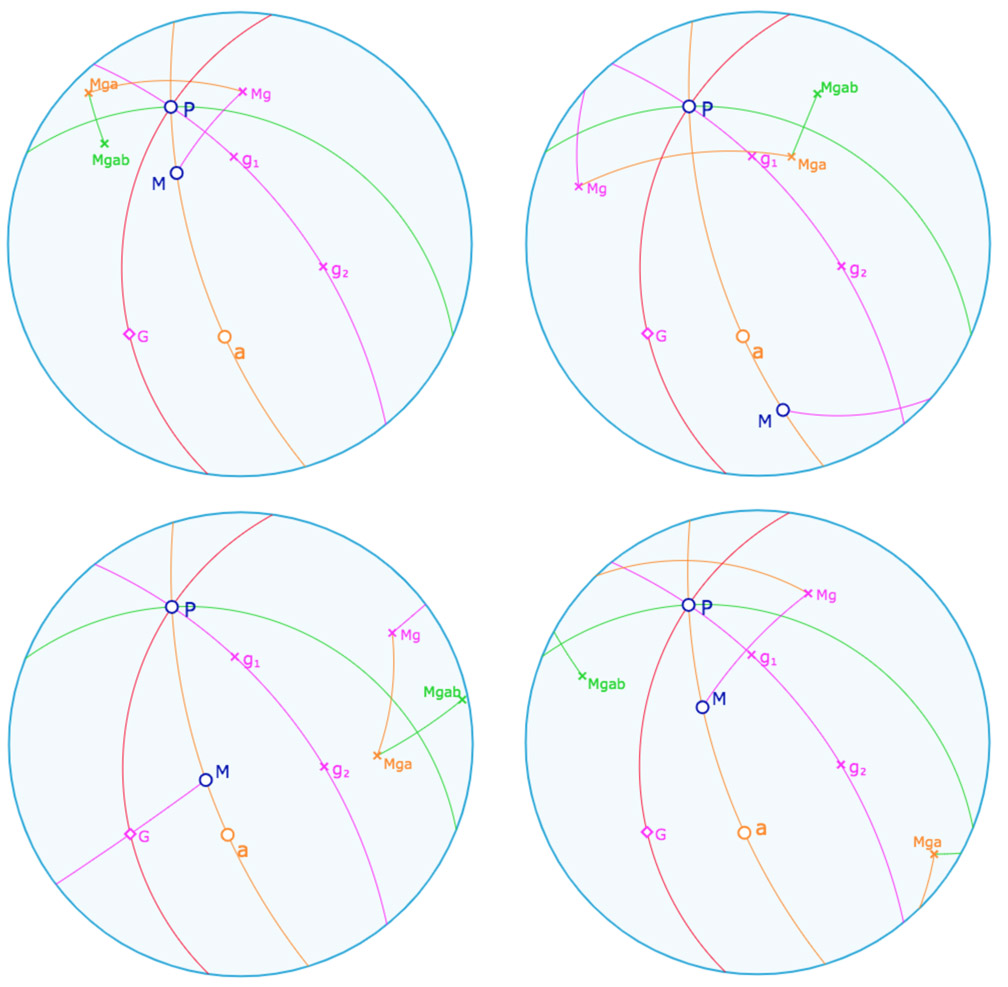
Dans ces 4 illustrations, on a simplement déplacé \(M\) sur la droite \(a\).
En haut à gauche : les trois segments sont « intérieurs », les symétries se comportent comme des pliages – qu’elles ne sont pas.
En haut à droite, le segment \([M \, Mg]\) est « extérieur », la symétrie orthogonale se comporte comme une symétrie centrale de centre \(G\), le pôle de \(q\).
En bas à gauche, c’est la symétrie par rapport à \(a\) qui se comporte comme une symétrie centrale, on repère visuellement le pôle de \(a\) à l’intersection de la droite verte et le segment orange \([Mg \, Mga]\).
En bas à droite , seule la première symétrie à un comportement usuel de symétrie orthogonale.
La figure à manipuler est proposée plus loin.
Cas 2 : \(P\) n’est pas incident à \(g\)
Alors deux sous-cas sont possibles
Soit \(P\) est différente de son image par \(g\) : \(P \neq Q=P^g\).
Soit \(P=g\) : le point et la droite sont pôle et polaire l’un de l’autre.
2.a .Supposons que \(P\) et \(Q\) soient différents.
Alors de par l’axiome 1, il existe une droite \(h\) telle que \(P, Q \mid h\). Alors par l’application de g – involutive, \(Q^g=P\) – il en résulte que \(Q, P \mid h^g=q\). On est donc dans le contexte où \(P, Q \mid h, q\) avec \(Q \neq P\). Alors l’axiome A2 assure que \(h=q\). Il en résulte que \(h\) est globalement invariante par \(g\).
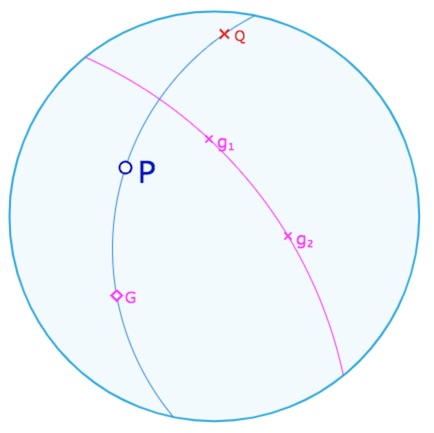
Or comme \(h\) et \(g\) sont différentes (puisque \(P \mid h\) et que la relation n’est pas vraie pour \(g\)) la seule possibilité est \(h \mid g\) car nous avons vu dans le paragraphe sur les collinéations, que les seules droites globalement invariantes par une réflexion orthogonale, outre l’axe de la symétrie, sont les droites orthogonales à l’axe : \(h\) est bien la droite cherchée.
2.b. Supposons \(P=g\)
\(P\) et \(g\) sont pôle et polaire l’un de l’autre. Dans l’illustration suivante, cela signifie que le point \(P\) est confondu avec le pôle \(G\) de \(g\). Alors pour toute droite \(c\) telle que \(c \mid P\), on a \(c \mid g\) (et réciproquement). Soient deux droites \(a\) et \(b\) telles que \(P=ab\). Par le théorème 1, on sait que l’on a la relation \(a,b \mid P\) et donc \(a,b \mid P\)g. Dans ce cas non seulement il existe une perpendiculaire, mais il en existe plus qu’une : toute droite incidente à \(P\) convient.
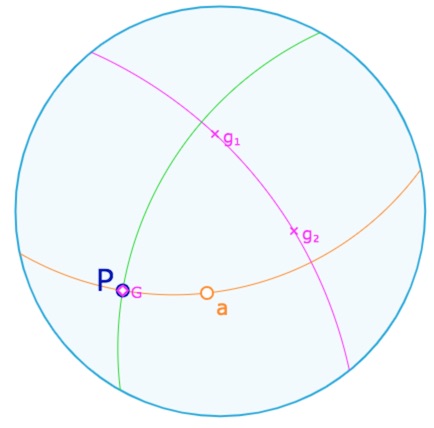
Figure manipulable contenant les trois cas précédents.
Placer d’abord le point \(P\) (sur \(g\), en dehors, et sur \(G\) grâce aux aimantations), puis le point \(M\) sur la droite \(a\).
On peut ensuite déplacer les points \(a\), \(g_1\) et \(g_2\).
Dans tous les cas, on peut appeler le point \(gh\) pied de la perpendiculaire \(h\) issue de \(P\). C’est un point de \(g\). Le théorème suivant montre que le cas 2.b est le seul cas où la perpendiculaire n’est pas unique.
Th 4 : unicité de la perpendiculaire
Soient \(P\) et \(g\) tels que \(P \neq g\). Si \(P \mid a,b\) et \(a, b \mid g\), alors \(a = b\).
La perpendiculaire du théorème précédent est unique dans le cas où le point n’est pas le pôle de la droite.
Il s’agit de montrer que si deux droites passent par \(P\) et sont toutes les deux orthogonales à une droite \(g\) non polaire de \(P\), alors ces deux droites sont confondues.
Cas 1 – \(P\) est incident à \(g\) : on \(P \mid g\). Comme par hypothèse \(a \mid P\) et \(a \mid g\) , le théorème 1 permet de dire que \(P=ag\). Pour la même raison \(P=bg\). On a donc \(ag=bg\), soit \(a = b\).
Cas 2 – \(P\) n’est pas incident à \(g\) . Alors, puisque nous sommes dans le cas où \(P\) n’est pas le pôle de \(g\), nécessairement \(Q=P^g \neq P\) . Par hypothèse \(a,b \mid P\). La conservation de l’incidence par une collinéation donne \(a^g,b^g \mid Q\). Or puisque \(g\) est orthogonale à la droite \(a\), \(a^g=a\). De même \(b^g=b\). Il en résulte donc que \(a,b \mid P, Q\). Comme \(P\) et \(Q\) sont deux points distincts, par l’axiome 2, les droites \(a\) et \(b\) sont confondues.
Th 5 : Toute droite d’un plan métrique de Bachmann est incidente à au moins trois points.
Nous allons démontrer ce résultat en plusieurs étapes, et pour cela nous utiliserons l’axiome A5, c’est-à-dire l’existence de trois droites \(g, h, j\) telles que \(g\) et \(h\) soient orthogonales, alors que \(j\) n’est ni orthogonale à \(g\) et à \(g\) et ni incidente au point \(g\)h.
Étape 1 – Lemme: si une droite \(a\) est incidente à 3 points, toute droite non perpendiculaire à \(a\) est aussi incidente à 3 points.
Preuve de ce lemme : Soient \(M, N\) et \(P\) trois points incidents à \(a\) et soit \(b\) une droite non orthogonale à \(P\). Alors il existe, sur \(P\), les points \(h_N, h_P\), pieds des perpendiculaires à \(b\) issues de \(M, N\). Montrons par l’absurde que ces trois points sont distincts. En effet si deux points sont confondus, cela signifie qu’en ce point (de \(b\)) il existe deux perpendiculaires à \(b\) issues d’un point de \(a\). Par le théorème 4 ces deux droites sont égales, et par l’axiome 2, elles sont égales à la droite \(a\). Ce qui contredit l’hypothèse que \(a\) n’est pas orthogonale à \(b\).
Illustration de l’étape 1 … dans le cas elliptique
Dans cette figure, on peut agir sur les poignées \(a_1, \, a_2\) de la droite \(a\) ou les poignées \(b_1, \, b_2\) de la droite \(b\) et déplacer les trois points \(M, N, P\) de \(a\)
Pieds des perpendiculaires de trois points distincts :
Manipulation : déplacer la poignée \(b_2\) (aimantée …) pour que la droite \(b\) passe par le pôle \(A\) de \(a\).
C’est le seul cas où les trois pieds des perpendiculaires sont confondus.
Étape 2 – S’il existe une droite incidente à 3 points toute droite est alors incidente à 3 points (au moins).
D’une part, d’après le lemme ci-dessus, si une des trois droites \(g, h\) ou \(j\) de l’axiome A5 est incidente à trois points, il en résulte que les trois le seront.
D’autre part, considérons une droite quelconque \(a\). Remarquons qu’elle ne peut être orthogonale aux trois droites \(g, h, j\) de l’axiome A5. En effet, si \(a\) est orthogonale aux trois droites, elle l’est en particulier pour \(g\) et \(h\) (orthogonales entre elles) et donc, par le théorème 2, on en déduit que \(agh=1\) soit encore \(a=gh\). On aurait alors que \(gh \mid j\) ce qui est contraire à l’hypothèse de l’axiome A5.
Donc si une droite \(a\) est incidente à 3 points, il en est de même des trois droites de l’axiome A5 puisque c’est vrai au moins pour l’une d’elle. Une droite quelconque \(b\) ne pouvant être elle aussi orthogonale aux trois droites \(g, h, j\), il en résulte qu’elle aussi contient au moins trois points.
Illustration dynamique de cette partie 2 (ci-dessous copie d’écran de la figure)
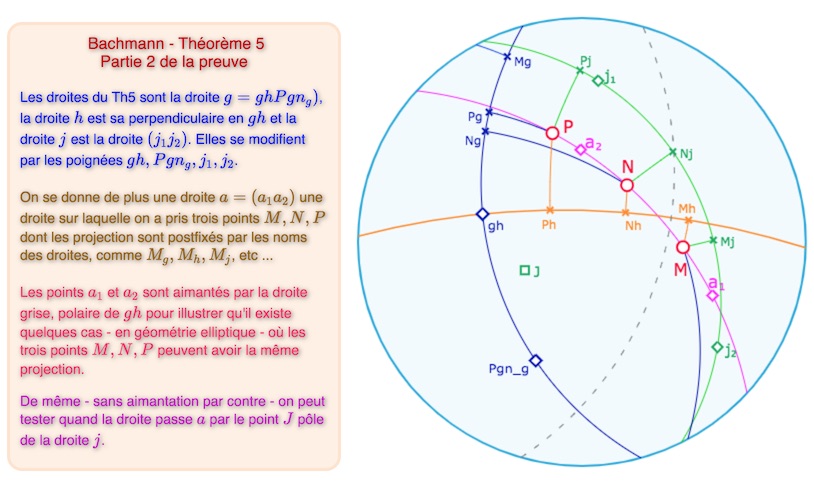
Ouvrir cette figure dans un nouvel onglet.
Étape 3 – Construction d’une droite incidente à trois points distincts.
Considérons la droite \(l\), la perpendiculaire à \(j\) issue de \(gh\). On peut parler de « la perpendiculaire » car \(j\) n’étant pas orthogonale à \(h\), on est assuré que le point \(gh\) n’est pas égal à \(j\) (car \(gh=j\) aboutit à \(hj=g\) et donc \(h \mid j\) ce qui n’est pas) il y a donc unicité par le théorème 4. Cette droite \(l\) est incidente aux points \(gh\), et \(lj\), mais aussi à son symétrique \((lj)^{gh}\). Pour montrer cette troisième incidence, on remarque que la symétrie centrale par rapport à \(gh\) est aussi la symétrie orthogonale par rapport à sa polaire (droite grise ci-dessous) pour laquelle on a vu que la perpendiculaire \(l\) est globalement invariante. Reste à voir que ces trois points sont bien deux à deux distincts.
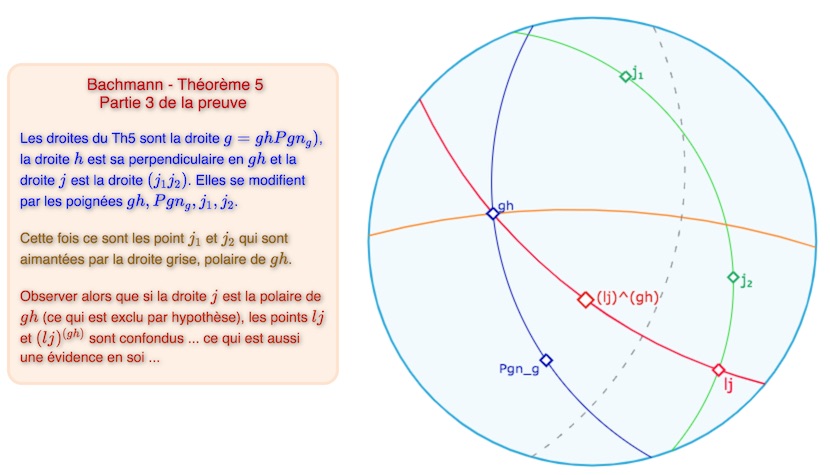
Ouvrir cette figure dans un nouvel onglet.
\(gh \; \mathrm{et} \; lj\). Ces deux points sont distincts tout simplement parce que \(j\) est incidente à \(lj\) et pas à \(gh\).
\(gh \; \mathrm{et} \; (lj)^{gh}\). Comme \(gh\) et \(lj\) sont différents par application de la bijection \(gh\), on peut dire que \( (gh)^{gh}\) et \( (lj)^{gh}\) sont différents et donc que \(gh\) est différent de \( (lj)^{gh}\).
\(lj \; \mathrm{et} \; (lj)^{gh}\). On a que \( (lj)^{gh}=l^{gh}g^{gh}=l \, j^{gh}\) car \( l^{gh}=l\). Donc si il y avait égalité entre \(lj\) et \( (lj)^{gh}\), on aurait aussi \(j=j^{gh}\). Ce qui signifie que soit \(gh \mid j\) soit que \(gh=j\)j. Le premier cas est exclu dans l’axiome A5, le second aussi comme vu au début de cette étape 3 (et testé dans la figure ci-dessus).
Ainsi ces trois points sont bien à deux distincts : nous avons trouvé trois points sur la perpendiculaire à \(j\) issue de \(gh\) dans les droites de l’axiome A5. Ceci prouve que, dans le système d’axiomes de Bachmann, toute droite a au moins trois points.
Conséquences et réciproques des axiomes de tri-réflexions
Les 4 théorèmes suivants
Nous nous intéressons maintenant spécifiquement aux propriétés des droites des deux axiomes de tri-réflexions.
Th 6 : Complément à l’axiome 3
\((P \mid a, b, c) \; \mathrm{et} \; (d=abc) \quad \Longrightarrow \quad P \mid d \)
Si \(P\) est incident à trois droites \(a, b,\) et \(c\), alors \(P\) est incident à leur produit.
Preuve : On sait que (\(P\) est incident à \(a\)) ssi (\(abcP=Pabc\)) et (\(abc\) différent de \(P\))
La première assertion \(abcP=Pabc\) est vraie car \(P\) étant incident à chaque droite, \(P\) commute avec chacune d’elle : \(Pa=aP\),\(P\)b=bP et \(Pc=cP\). La commutativité de \(P\) et du produit \(abc\) en découle.
Montrons la seconde assertion par l’absurde. Supposons que \(abc=P\), alors \(ab=Pc\) et comme \(P \mid c\), \(Pc\) est d’ordre 2 et donc \(a \mid b\). Par le théorème 1, comme \(a,b \mid P\) et \(a \mid b\), il vient \(ab=P\). Donc \(Pc=P\) soit \(c=1\), ce qui est absurde.
Th 7 : Complément à l’axiome 4
\((g \mid a, b, c) \; \mathrm{et} \; (d=abc) \quad \Longrightarrow \quad g \mid d \)
Si \(g\) est orthogonale à trois droites \(a, b,\) et \(c\), alors \(g\) est aussi orthogonale à leur produit.
Preuve
\( d \perp g \quad ssi \quad (d \mid g) \; \mathrm{et} \; (d \neq ,g)\)
Comme ci-dessus la première assertion vient de la commutativité de \(d\) avec chacune des droites \(a, b, \) et \(c\) : elle est donc commutative avec le produit.
Montrons la seconde assertion également par l’absurde : si \(d=g\), on aurait \(a, b, c \mid abc\), soit à la fois \(a \mid b, \; b \mid c, \; c \mid a\) et donc, par le théorème 2, \(abc=1\), soit \(d=1\) ce qui est absurde puisque \(d\) est une droite.
Figure d’illustration des Th 6 et 7
Dans cette figure, les droites \(a\) et \(b\) sont manipulables par leurs poignées \(a_1, a_2\) et \(b_1, b_2\), la droite \(c\) par l’unique point \(c_1\) car elle appartient au pinceau \(P_{ab}\) (la construction sera présentée ultérieurement). On construit la droite rouge \(d=abc\) qui est, soit incidente à \(P\) si ce point est incident à \(a,b, \; \mathrm{et} \; c\) soit orthogonale à la perpendiculaire commune (marron) à ces trois droites.
Depuis un point \(M\) on construit \(a^M\) son image par \(a\), puis \(ab^M\), l’image de ce point par \(b\) et enfin \(abc^M\) l’image par \(c\). La droite \(d=abc\) est alors la médiatrice de \(M\) et de \(abc^M\). On a ensuite tracé (en mauve) soit l’équidistante à la perpendiculaire commune passant par \(M\), soit le cercle de centre \(P\) passant par \(M\).
En déplaçant \(M\), observer que la droite rouge est bien invariante, et donc propre aux droites \(a, b, c\),
et ceci indépendamment de la nature du pinceau \(P_{ab}\) de ces droites.
Préférer ouvrir cette figure (plus grande) dans un nouvel onglet.
Th 8 : Réciproque de l’axiome 3
Pour \(a, b\) soit \(c\) tel que \(abc \in \Delta\). Si \(P \mid a, b\) alors \(P \mid c\).
Si un point est incident à deux droites distinctes, toute droite en pinceau avec elles est aussi incidente à ce point.
Preuve
Soit \(g\) une perpendiculaire à \(c\) incidente à \(P\). Notons \(Q=gc\). Nous voulons montrer que \(P=Q\). On sait que \(Q\) est incident à \(g\) et \(c\).
Les trois droites \(a ,b ,\) et \(g\) sont incidentes à \(P\). L’axiome 3 assure qu’il existe une droite \(h\)telle que \(abg=h\), et le complément de l’axiome 3 permet de préciser que \(P\) est incident à \(h\) puisque c’est le cas des trois droites. De plus, puisque \(a\) et \(b\) sont distinctes, \(h\) et \(g\) le sont aussi.
Mais \(hgc=abggc=abc=d \in \Delta\), et donc \(gc=hd\) soit \(hd=Q\). Or le théorème 1 permet d’en déduire que \(Q\) est incident à \(h\) (et \(d \mid h\)).
On a donc \(P, Q \mid g, h\)). avec \(g\) et \(h\) distinctes : par l’axiome 2, on en déduit que \(P=Q\) et donc \(P\) incident à \(c\).
Illlustration de la preuve (environnement hyperbolique)
Dans l’image de gauche, la droite \(c\) n’est pas en pinceau avec les droites \(a\) et \(b\), et donc \(Q\) est distinct de \(P\). Les droites \(g\) et \(h\) existent et sont bien construites. Par contre la droite \(d\) n’existe pas (le produit \(abc\) n’est pas une droite).
Dans l’image de droite, la droite \(c\) vérifie bien la condition de l’hypothèse \(abc \in \Delta\), alors \(P\) et \(Q\) sont confondus et on a bien \(Q=hd\), c’est-à-dire \(h \mid d\).
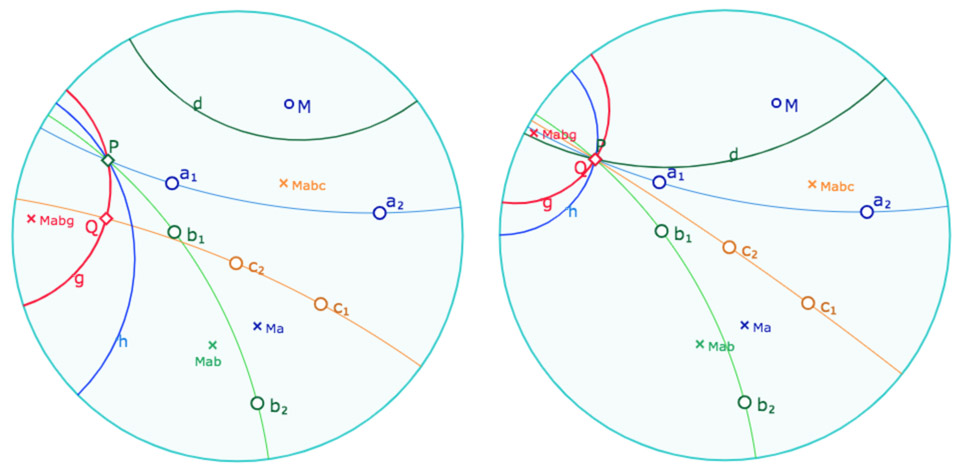
Ici \(h\) est construite comme médiatrice de \(M\) et \(M^{abg}\),
et \(d\) comme médiatrice de \(M\) et \(M^{abc}\) (alors que \(abc\) n’est pas une droite).
Th 9 : Réciproque de l’axiome 4
Pour \(a \neq b\) soit \(c\) tel que \(abc \in \Delta\). Si \(g \mid a, b\) alors \(g \mid c\).
Si une droite est orthogonale à deux droites distinctes, toute droite en pinceau avec ces deux droites est aussi orthogonale à la première.
Soient \(a\) et \(b\) deux droites distinctes et \(g\) une perpendiculaire commune à \(a\) et \(b\). Si \(c\) est une droite telle que le produit \(abc\) soit une droite \(d\), on veut montrer que \(g\) est perpendiculaire à \(c\).
En préliminaire, remarquons qu’avec les hypothèses, on ne peut avoir \(c=g\). En effet, nous avons \(a \mid g\) et \(b \mid g\). Si \(abg\) était une droite, on aurait – faire le calcul – aussi \(a \mid b\). Et donc \(abg\) serait égal à 1 par le théorème 2 : ce ne serait pas une droite.
Soit \(P\) un point arbitraire incident à \(c\) : on a \(c \mid P\) d’ordre 2. Regardons tout d’abord le cas particulier où \(P\) serait égal à \(g\) : si\(P=g\), on a \(c \mid g\) et donc \(c\) orthogonale à \(g\) (car \(c=g\) a été exclu dans le préliminaire).
Nous sommes donc maintenant dans le cas où \(P\) est différent de \(g\). Alors par \(P\) il existe une unique perpendiculaire à \(g\), que nous nommerons \(h\). Il s’agit de montrer que \(h=c\).
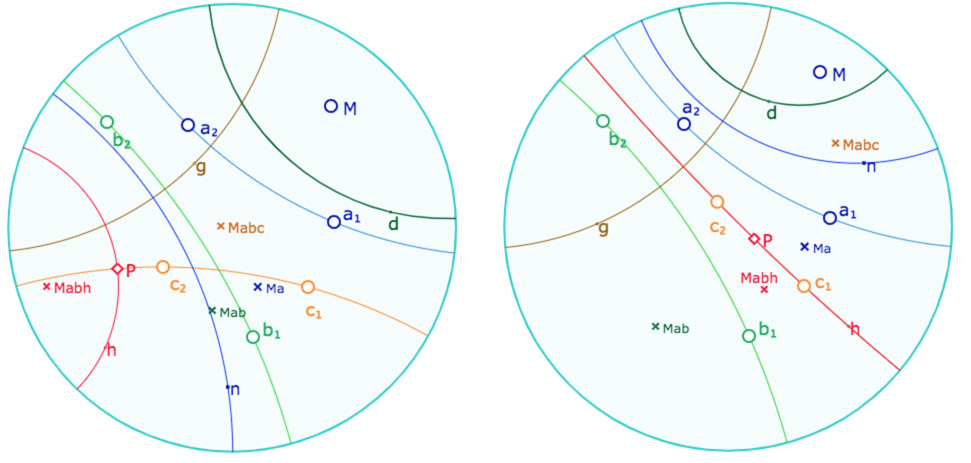
à gauche : le cas où la droite \(c\) ne vérifie pas \(abc \in \Delta\) (et donc \(d\) n’est pas la droite \(abc\).
à droite : on a bien \(abc \in \Delta\), et on voit que \(h\) se superpose à \(c\).
Tout d’abord, puisque \(a, b\) et \(h\) sont toutes trois orthogonales à \(h\), l’axiome 4 permet de dire que \(abh\) est une droite \(n\), et le complément à l’axiome 4 (Théorème 7) précise que \(n\) est aussi orthogonale à \(g\). Il en résulte que \(dc=ab=nh\) et donc \(chn=d\).
Supposons que \(c\) soit différente de \(h\), on peut appliquer le théorème 8 à la situation : \(P\) est incident à \(c\) et \(h\), et comme \(chn\) est une droite, il en résulte que \(P\) est aussi incident à \(n\).
Ainsi, \(P\) est incident à \(h\) et \(n\). De plus \(P\) est différent de \(g\), et \(g\) est orthogonale à \(h\) et \(n\). D’après le théorème 4 – l’unicité de la perpendiculaire à une droite (\(g\)) issue d’un point (\(P\)) qui lui est différent – les droites \(h\) et \(n\) sont égales, d’où \(ab=nh=hh=1\) soit \(a=b\), ce qui est exclu par hypothèse. Donc \(c=h\).
Avec ces neuf théorèmes, nous avons fait le tour des premières conséquences immédiates du système d’axiome des plans métriques. Dans les pages suivantes nous abordons de « vrais » théorèmes.