Dans ce menu on s’intéresse à une autre surface pseudosphérique, celle dite « hyperbolique » (PSH dans la suite) car elle a deux points de contact avec l’infini. La partie du plan hyperbolique recouverte par la feuille principale étant nettement plus grande que pour la pseudosphère (PS), on va pouvoir aborder des questions, et réaliser des figures qu’il n’était pas envisageable de construire sur la pseudosphère initiale. Ainsi, comme, d’une certaine façon on va aller plus loin dans la complexité des figures (en terme de lieux de points pour tracer des segments), on sera attentif au départ à bien optimiser les étapes de constructions.
Cette page d’introduction est essentiellement consacrée à la construction dynamique de la nappe de cette surface. C’est finalement la seule chose délicate à réaliser, car la génératrice est donnée par une intégrale elliptique. Et donc il s’agit de réaliser une approximation fiable et robuste de cette surface.
La lecture de ce menu suppose, a priori, d’avoir pris connaissance des pages sur la pseudosphère, et en particulier des pages à partir de la conjugaison avec KB.
Approximation de la surface
On se donne un paramètre \(p\) , réel positif, la courbe de la surface dans le plan frontal – la génératrice – est donnée par la relation \(\left\lbrace \begin{array}{1} x(u) = p \, ch(u)\\ z(u) = \displaystyle \int_0^u \sqrt{1-p^2sh^2(t)} \,dt\end{array} \right.\) avec \(-sh^{-1}\displaystyle \left( \frac{1}{p} \right) \le u \le sh^{-1}\displaystyle \left( \frac{1}{p} \right)\)
Ce qui motive de travailler sur une approximation précise de cette génératrice est que les correspondances dans le « disque limite » de Beltrami (le modèle KB) ne font intervenir l’intégrale elliptique que par sa dérivée et donc qu’elle disparaît. Ainsi, le passage de la PSH \((u, \theta)\) vers KB \((x, y)\) est donné par \(\left\lbrace \begin{array}{1} x= th(p\theta)\\ y=\displaystyle \frac{th(u)}{ch(p \theta)}\end{array} \right.\)
et le retour est immédiat à traiter aussi.
Les données mathématiques sur la PSH et la PSE proviennent de : Modern Differential Geometry of curves and surfaces with Mathematica – Alfred Gray – 1997 (2° Ed.). En particulier le chapitre 19 : Surfaces of constant gaussian curvature.
Il existe désormais une 3° édition, avec illustrations en couleurs.
La démarche de réalisation des figures est donc la suivante : à partir d’une latitude \(u\) et d’un angle \(\theta\) exacts, on construit une représentation d’un point, plus généralement d’un objet, approchée. La transformation dans le modèle KB est exacte, les constructions y sont faites, la transformation réciproque donne des coordonnées exactes des objets à construire qui sont faits dans la même approximation que les objets de départ.
Le polynôme final retenu – après de nombreux essais sur le nombre de points, leur positions, entre autre – est obtenu par double interpolation de Lagrange : d’abord par rapport à la latitude \(u\) avec 7 points correspondant à la demi-longueur de l’intervalle de définition multipliée par -1, -0.9, -0.5, 0, 0.5, 0.9, 1 puis, pour chaque coefficient, par rapport à \(p\) avec les valeurs \(p\) = 0.25, 0.5, 0.75, 1, 1.25
En pratique, pour des valeurs de \(p\) dans l’intervalle d’interpolation, les résultats sont remarquables. Voici trois copies d’écran, pour trois valeurs de \(p\), de la génératrice « exacte » (calculée avec Mathematica) superposée à celle de l’interpolation de Lagrange :
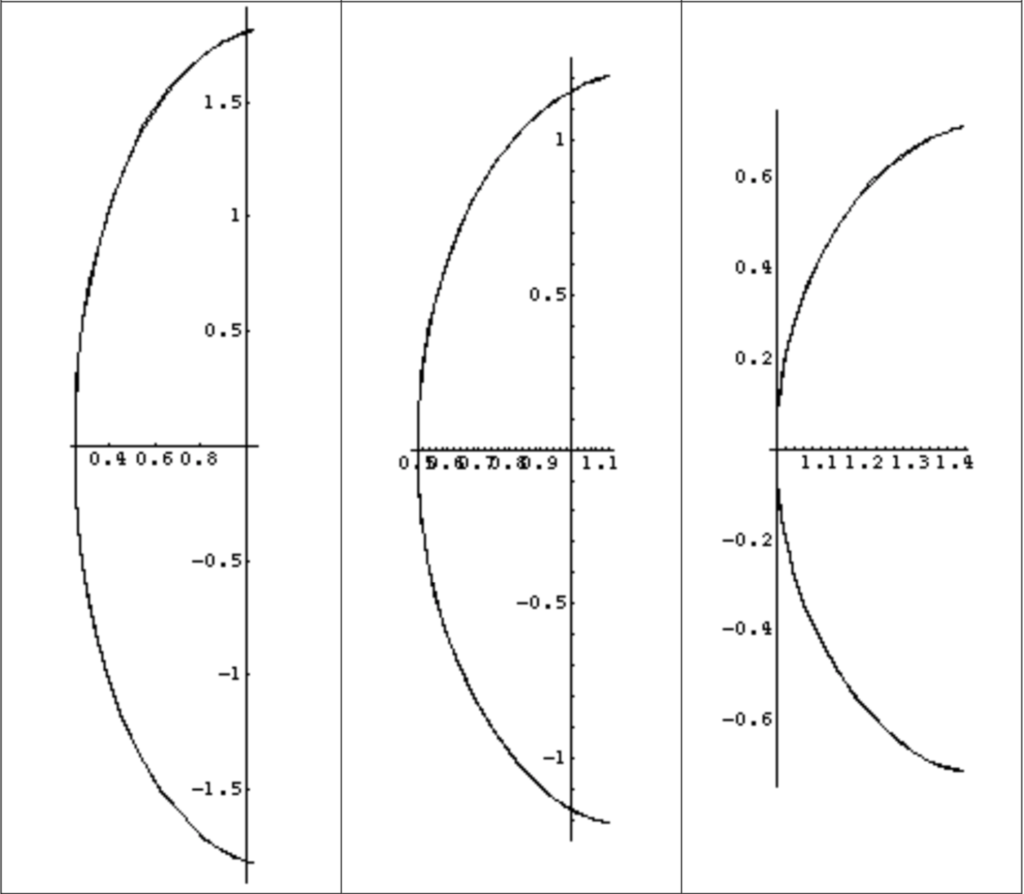
à gauche, \(p\)=0,25 – au centre, \(p\)=0,5 – à droite, \(p\)=1,25
En pratique l’approximation est de l’ordre du quart de pixel sauf aux toutes extrémités de la nappe où elle est de l’ordre de un ou deux pixels.
Le polygone obtenu pour la génératrice
g(u)=(- 0,102319 p4 – 0,0138416 p3 – 0,0870262 p2 – 0,0124497 p – 0,000789732) u5
+ (- 0,00863112 p4 + 0,0368179 p3 – 0,159956 p2 + 0,0582975 p + 0,0133804) u3
+ (- 0,0115381 p4 + 0,0459398 p3 – 0,071502 p2+ 0,0547965 p + 0,96737) u
ce que l’on écrira sous la forme \(g(u)= \left(Coef_{p5}u^4+Coef_{p3}u^2+Coef_{p1} \right)u\) où les coefficients ne dépendent que de \(p\) et ne sont recalculés – une seule fois pour toute la figure – que si on modifié le paramètre.
Construction effective de la PSH
Voici un concentré des données utiles à la construction
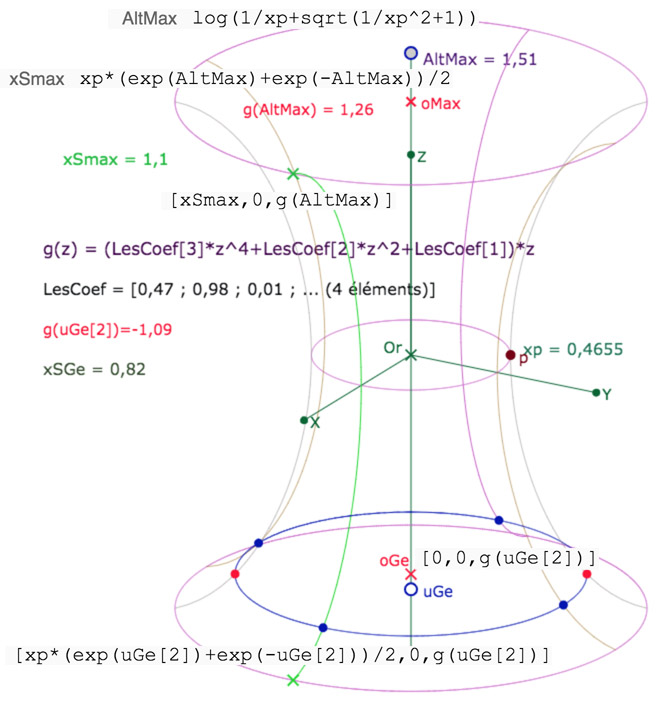
L’origine du repère s’appelle \(Or\) (pour que le nom \(O\) puisse être utilisé dans les figures). Le point \(p\) est, à la fois, un point de la surface 3D et un point en 2D, qui reste fixe quand la surface tourne. C’est pour cela qu’on ne peut pas montrer ce point dans les macros, et que l’on utilisera toujours son abscisse \(xp\), qui est le coef \(p\) des formules. Les coefficients de la fonction \(g\) sont placés dans une liste, pour passer plus rapidement en macro :
LesCoef = [xp, Coefp1, Coefp3, Coefp5].
Dans cette présentation, on a tracé 6 génératrices, deux sur l’axe \((Ox)\), une verte, une mauve, deux sur l’axe \((Oy)\) (marron clair) et deux, grises, qui sont toujours dans le plan frontal (générés par les points rouges sur le cercle de centre \(oGe\)) . Dans les figures des pages suivantes, on enlèvera parfois les génératrices en \((Oy)\) car ce n’est pas nécessaire quand il y a de figures sur la surface. Le tout est généré par le point \(uGe\).
Quelques illustrations en fonction du paramètre \(p\)
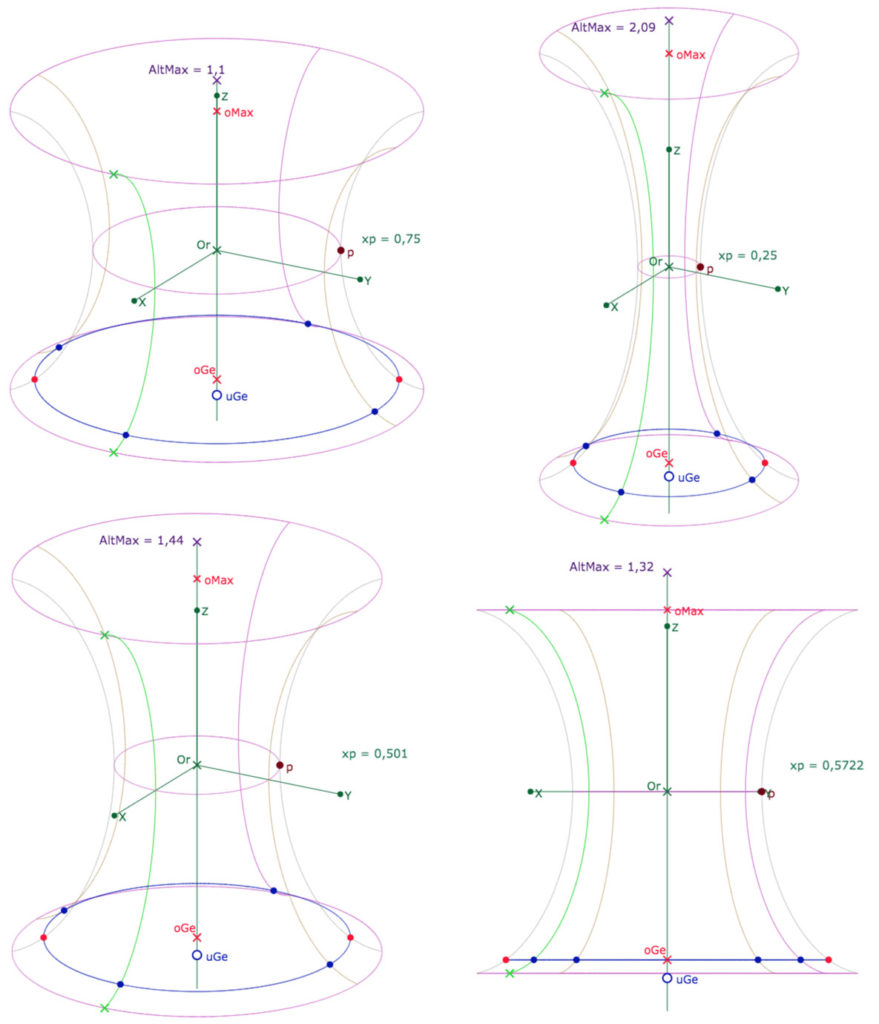
Manipuler une première figure de base
Agir sur \(p\) et \(uGe\). Observer qu’on peut facilement être – perceptivement – dans un repère indirect.
Préférer ouvrir cette figure (hors restriction) dans un nouvelle onglet.
La représentation de la PSH dans KB
On veut maintenant placer des points sur la PSH et les envoyer sur KB avec la projection de Beltrami. La macro de construction de l’horicycle parallèle à l’équateur de la pseudosphère, se transforme simplement pour la PSH, en prenant comme objets initiaux, la liste des coefficients et la fonction \(g\). Mais on remarquera surtout, dans le nom des macros de l’illustration suivante, que l’horicycle est devenue une équidistante puisque la courbe a deux points à l’infini, nommés en \(Idl\) et \(Jdl\). Le calcul du passage de la PSH à KB se fait en une seule ligne.
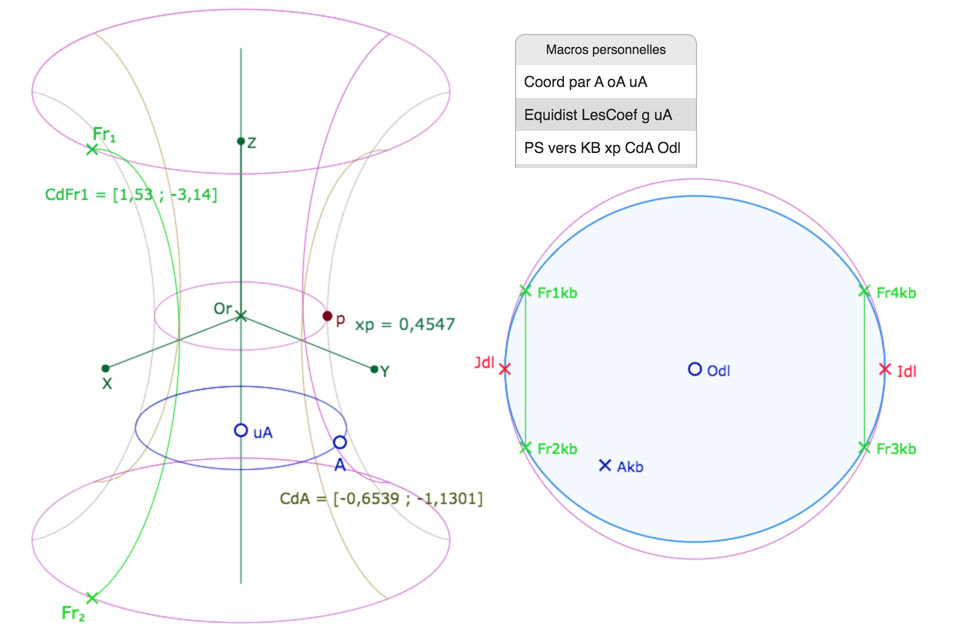
Dans KB, en bleu l’équidistante de projection de la PSH. En vert les limites de la feuille principale paramétrée sur [-π,π[.
On notera que, selon les macros, on donne en objets initiaux, soit seulement la valeur numérique \(xp\), soit la liste des coefficients et la fonction \(g\) (pour éviter de la reconstruire à chaque fois). C’est moins « transparent » que dans le cas de la PS mais c’est aussi nettement plus optimisé pour éviter les objets intermédiaires inutiles.
Le méridien vert est l’origine – et l’extrémité – de la feuille principale. Pour couvrir une plus grande partie du plan hyperbolique dans sa projection sur KB, on choisit de la paramétrer de \(-\pi\) à \(\pi\). Le paramètre \(p\) modifie sensiblement la couverture de la feuille principale :
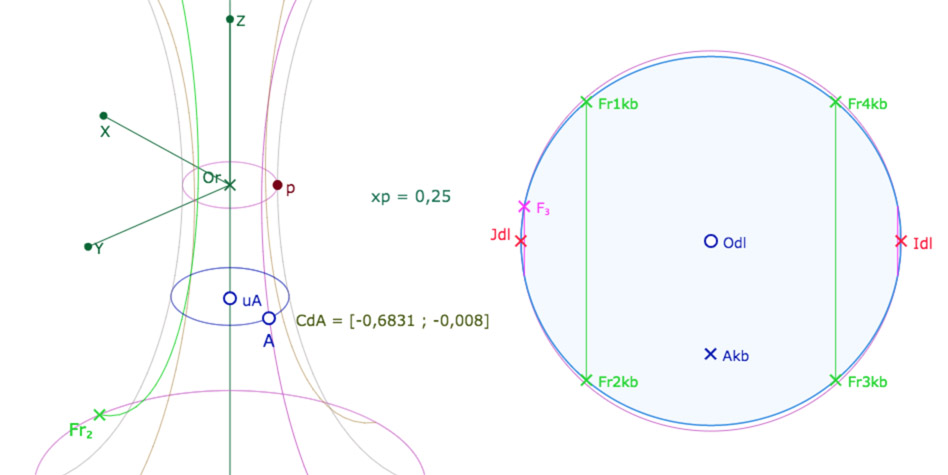
Dans cette illustration on voit que, pour \(p=0,25\) la PSH recouvre presque tout le plan hyperbolique
Le point \(F_3\) et les segments verticaux roses marquent la frontière avec les feuilles 2 et 3.
On a chosit de placer \(A\) quasiment sur le méridien opposé à celui de l’origine (\(\theta=-0,008\)).
On voit que son image est « quasi » sur la verticale issue du centre du cercle.
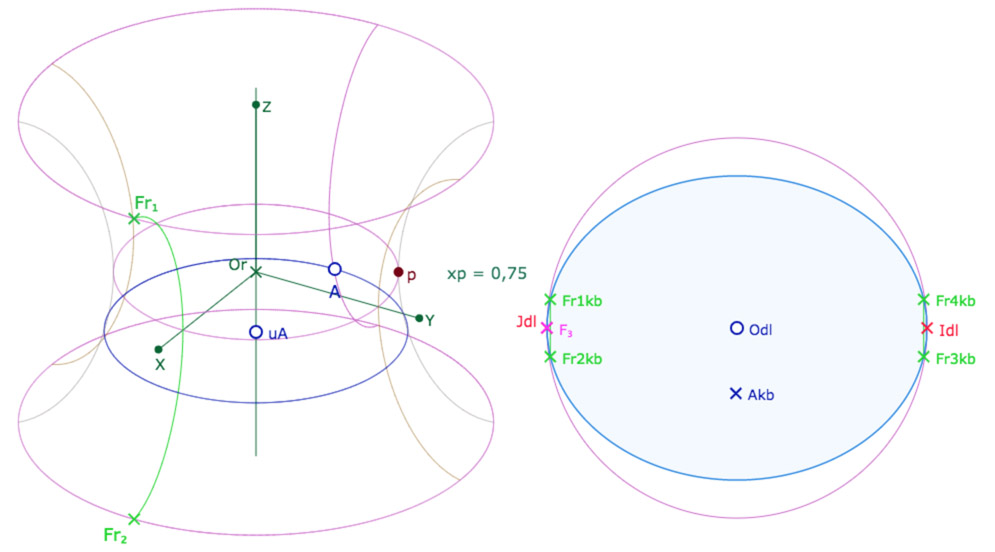
Par contre pour \(p=0,75\), il n’y a pratiquement plus de déploiement visible des feuilles autour de la feuille principale.
Présentation du menu PSH
L’essentiel du travail effectué est centré sur les pavages hyperboliques. Sur une nappe comme la PSH, qui s’enroule sur elle-même et qui ne recouvre pas tout le plan hyperbolique, on entendra par pavage uniquement la réalisation de polygones autour d’un point (ce n’est donc pas un pavage du plan, juste le tout début de la première génération. Mais déjà faire entrer cette construction entièrement sur la nappe, pour certains pavages, est un vrai objectif en soi. Avant d’aborder les pavages, deux premiers menus reviennent sur les constructions classiques de base.
Le menu se termine par deux pages sur la PSE (pseudosphère elliptique)
Droites et premières figures
On aborde la construction générale d’une droite sur la PSH. Puis on voit la difficulté de ne construire que des droites multifeuilles. On présentera les macros de KB qui permettent de ne construire que les traces des droites sur la feuille principale.
Cet item de menu présente les médianes, hauteurs, médiatrices et bissectrices d’un triangle (cercles exinscrits).
Trilatères – deux figures
On propose deux figures classiques pour les trilatères : les hauteurs et le cercle inscrit du triangle podaire, puis la traditionnelle construction de Malfatti sur la PSH (qui se fait rapidement après la construction sur la PS).
Pavage P54 (de pentagones orthogonaux) et P45 de carrés à 72°
Comme signalé en introduction, il s’agit de construire, autour d’un point, 4 pentagones orthogonaux. On commence par ce pavage car comme le pentagone orthogonal a été fait sur la PS, on peut utiliser les constructions dans KB en les transformant en macro-construction. C’est l’occasion de voir que la réalisation effective sur la surface dépend du paramètre \(p\). C’est alors une belle illustration de ce que ces surfaces, pour des valeurs différentes de \(p\) ne sont pas isométriques
Pavage P46 (de carrés à 60°) et P64 (d’hexagones orthogonaux)
Ces pavages sont l’occasion de réaliser surtout de belles figures « extraites » du pavage.
Pavage P38 et P83
Placer 8 triangles de 45° autour d’un point s’avère plus délicat que les précédents pavages, il faudra choir des paramètre bien précis, alors qu’au contraire, placer 3 octogones autour d’un point ne pose aucune difficulté. Et là aussi, ces deux pavages sont surtout l’occasion de faire de belles illustrations d’objets que l’on n’a pas l’habitude de rencontrer.
Approche de P48 et P84
Le carré de P(4,8) est celui de la quadrature hyperbolique du cercle. Mais le rayon du cercle de pavage de P(4,8) est trop grand pour faire entrer ce pavage sur la pseudosphère – sauf peut-être à placer le cercle très loin sur la 4° feuille mais les techniques utilisées ici ne le permettent pas. On verra donc quelques figures d’exploration sur ce pavage, en particulier on pourra réaliser un demi-pavage.
PSE 1 – Nappe – Conjugaison – Premières figures sur la surface pseudosphérique elliptique
On reprend la même démarche sur cette surface. On aborde en détail la question des figures multifeuilles car le sens de cette question est particulier dans ce contexte de modèle borné. La page s’achève avec les constructions classiques
PSE 2 – Triangles – Trilatères
De très belles figures, en particulier sur les cercles inscrits de trilatères dits « tri-feuilles », et quelques configurations spécifiques à la PSE comme les triangles ayant pour orthocentre le point de singularité de la surface, ou encore le traditionnel pentagone orthogonal.