On rappelle que dans tous les menus de ce site, il est conseillé d’avoir lu en préalable la page associée au titre du menu lui-même, qui contient une présentation plus générale de ce menu..
Dans la lecture qu’il fait des travaux de ses prédécesseurs, Bachmann situe à 1933 la première présentation algébrique d’une axiomatique de la géométrie euclidienne, par Thomson, et à 1943 l’extension du travail précédent aux cas non euclidiens. Il ne manque pas de signaler les étapes initiales de ce travail de seconde axiomatisation – pour reprendre l’expression de Gonseth – que sont tout d’abord la démarche de Hessenberg qui, dès 1905, travaille sur les compositions de symétrie pour construire la géométrie, reprise plus systématiquement par Hjelmslev qui, à partir de 1907, montre ce que Bachmann appelle le théorème fondamental des plans métriques, et surtout, introduit la notion de demi-rotation pour plonger ces géométriques dans un plan projectif.
Dans sa démarche, Bachmann cherche un système d’axiome minimal, ce qui, bien entendu, engendre un nombre important de géométries (en particulier toutes les géométries finies qui ne peuvent pas être isomorphes). Bachmann va donc être amené à les classer et à mettre en évidence des axiomes spécifiques pour séparer ces géométries. Cette séparation donnera alors tout son sens « métrique » à la notion de droites parallèles.
Signalons, avant de poursuivre, le sens du mot métrique dans le vocabulaire de Bachmann. Il ne s’agit pas d’une notion attachée à une distance, c’est simplement un qualificatif pour un ensemble (en pratique un groupe) qui dispose d’axiomes minimaux qui feront de cet ensemble un plan muni d’une géométrie d’incidence et d’orthogonalité. Le choix de ce terme n’est pas particulièrement heureux, et il a d’ailleurs été souvent reproché à Bachmann, en références aux géométries déjà désignées de métriques par Cayley (puis Klein) en travaillant essentiellement, cette fois, sur une distance.
Lecture algébrique de l’orthogonalité et de l’incidence
Cette étape est une préparation à l’entrée dans la seconde axiomatisation de Gonseth. Bachmann, en nous invitant à observer des figures euclidiennes élémentaires avec un regard algébrique nous place de fait à ce second niveau : son domaine d’observation n’est pas le champ de l’expérience du monde sensible (des configurations), mais celui des transformations euclidiennes planes ; il nous invite donc à une perception structurelle.
Dans son regard algébrique, les objets de la géométrie, qui seront pour nous des droites et des points, vont être des transformations : des symétries orthogonales pour les premiers et des symétries centrales pour les seconds. La première figure décrit ce que sera un point, la seconde ce que va être l’incidence.
Composition de deux symétries orthogonales d’axes sécants
Définition algébrique de l’orthogonalité et du point
Dans la figure suivante, \(d\) et \(d’\) sont deux droites sécantes et \(M_1\) est l’image du point \(M\) par la composée \(s_{d’} o s_d\). Puis, par itération, on note \(M_{k+1}\) l’image de \(M_k\) par \(s_{d’} o s_d\). On sait que toutes ces images sont sur le cercle de centre l’intersection des deux droites et passant par \(M\). On se propose de visualiser quand cette composition est d’ordre 2 … même si tout le monde connait le résultat bien entendu.
Dans cette figure déplacer le point qui pilote la droite \(d’\) jusqu’à rendre les deux droites orthogonales
Le point nommé \(d’\) (poignée de la droite du même nom) est aimanté pour cela.
Il est aussi aimanté pour avoir une situation d’ordre 3 comme ci-dessous.
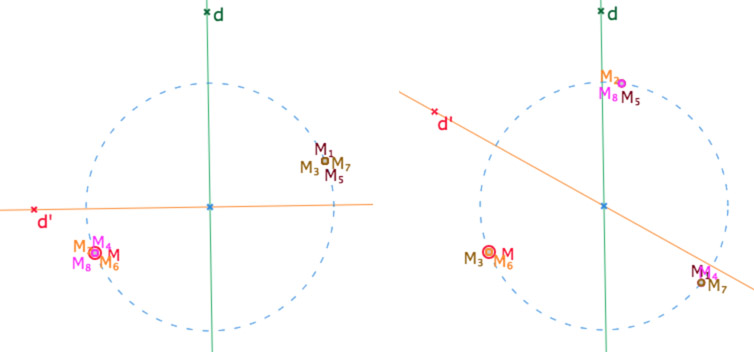
Copie d’écran de deux situations particulières. C’est bien entnedu celle de gauche qui nous intéresse.
On voit donc – dans le contexte euclidien – que quand deux droites sont orthogonales, la composée des deux est un élément d’ordre 2, en pratique une symétrie centrale. Cela induira deux définitions dans l’axiomatique de Bachmann dont voici une première approche :
Orthogonalité : deux droites sont dites orthogonales quand la composée des deux symétries orthogonales associées est d’ordre 2.
Point : on appellera point (ce sera une transformation) la composée de deux symétries orthogonales quand cette composée est d’ordre 2.
Et alors deux droites orthogonales sont sécantes en un point. Il faudra vérifier que ce point est indépendant des droites orthogonales sécantes en ce point. Cela découlera des autres axiomes.
Aspect algébrique de l’incidence d’une droite et d’un point
Soit \(d\) une droite et \(A\) un point. On s’intéresse à la composée \(s_d \; o \; s_A\) et plus particulièrement à quelle condition cette composée est d’ordre 2.
On introduit aussi, avec cette figure, la notation exponentielle postfixée, très utilisée par les auteurs allemands, pour la composition, et qui s’avère bien plus pratique pour le calcul algébrique comme il va être très utilisé ici. Ainsi \(s_d \; o \; s_A(M)\) se notera plus simplement \(M^{Ad}=(M^A)^d\). Les lecteurs … de ma génération … se rappelleront la notation « polonaise inversée » de certaines calculatrices. Pour les autres on revient plus en détail sur cette notation un peu plus loin, dans un bilan.
Dans la figure suivante, on a \(M_1=M^{Ad}\), et par itération \(M_{k+1}=M_k^{Ad}\). On sait – dans le contexte euclidien – que \(Ad\) est une symétrie glissée d’axe perpendiculaire à \(d\) et de vecteur de norme deux fois la distance entre le point et la droite. Par exemple la distance entre les points \(M_k\) et \(M_{k+2}\) est 4 fois celle entre \(A\) et \(d\).
Déplacer le point \(A\) pour le placer sur \(d\) (il y est légèrement aimanté).
Observer que la composée est alors d’ordre 2.
En effet, une symétrie glissée dontle vecteur est nul est tout simplement une symétrie orthogonale. Et ce sera la définition de l’incidence … à une nuance près qui sera développée quand cela sera nécessaire :
Incidence : un point \(d\) sera dit incident à une droite \(d\) si \((Ad)^2=1\).
Voyons une première conséquence immédiate. Ainsi \((Ad)^2=1\)s’écrit en particulier \(dA=Ad\) mais aussi \(dAd^{-1}=A\) et l’on voit poindre la conjugaison comme action du groupe sur lui-même : un point va être incident(*) à une droite si l’action de la droite sur le point le laisse invariant, mais aussi tout aussi bien l’inverse puisque \(AdA^{-1}=d\) : l’action du point sur la droite laisse celle-ci invariante.
(*) Cette démarche n’est pas vraiment nouvelle : dans les cours de géométrie amallagmatique [Deltheil & Caire], les points pouvaient être considérés comme des cercles de rayon nul et l’orthogonalité de ces cercles-points avec les autres était interprétée – et intervenait dans les calculs – comme une incidence. S’il y a une nouveauté ici, c’est dans le traitement totalement algébrique de ces notions.
Lecture algébrique des propriétés des symétries orthogonales
Les observations de la figure précédente nous donnent un regard algébrique sur les concepts d’orthogonalité et d’incidence. Pour construire une géométrie sur des bases aussi algébriques que ce qui précède, il faut maintenant dégager des propriétés essentielles sur les compositions des symétries orthogonales.
Bachmann a réussi à (re)construire toute la géométrie métrique – les principales géométries métriques – sur la base de deux propriétés, qu’il va choisir comme axiome : ce sont ses fameux axiomes de tri-réflexion, déjà étudiés par Hjelmslev. Si cette synthèse est remarquable de force et d’élégance, Bachmann lui-même l’insère dans le cheminement des travaux antérieurs sur les pinceaux. Nous avons vu que pour les deux géométries non euclidiennes étudiées, les droites remarquables d’un triangle, par exemple les médiatrices, ont quelque chose en commun, soit un point, soit une perpendiculaire (c’est la même chose dans le cas elliptique), soit encore (et alors c’est spécifique au cas hyperbolique) un point idéal, à l’infini.
Remarque de rédaction : dans une première version des menus DP et ELL, on avait écrit, de manière heuristique, qu’elles sont en faisceau, terme remplacé par pinceau depuis la mise en ligne de ce menu, mais qui peut exister encore dans les macros et dans quelques illustration. On reprend, dans ce menu, le vocabulaire de Bachmann, on dira que les droites sont en pinceau, terme objectivement plus approprié.
Ce fut l’expression d’une propriété, puis le terme a peu à peu glissé vers l’expression d’un objet mathématique. D’un certain point de vue, on peut dire que c’est sur la variabilité de cette expression « en pinceau » que Bachmann organise sa construction théorique. En effet, un contexte algébrique n’a aucune chance de rendre compte, dans ses axiomes, du troisième cas, celui des droites parallèles dans le cas hyperbolique. Pourtant il faut laisser émerger cette possibilité, et donc dégager une souplesse à une notion pour qu’elle aille au-delà des axiomes retenus. Cette souplesse sera dans sa définition, pour des droites, d’être en pinceau : au lieu de définir seulement des pinceaux de droites – et donc un nouvel objet – Bachmann s’intéresse à une propriété de ses objets premiers que sont les droites, et s’ouvre ainsi un champ des possibles éventuellement plus grand. Bien sûr les deux notions finiront par coïncider, mais plus loin dans la théorie, quand des propriétés élaborées des « droites en pinceaux » seront déjà bien structurées.
Bachmann s’intéresse donc aux triplets de droites qui ont soit un point soit une perpendiculaire en commun. Il s’y intéresse d’un point de vue algébrique bien entendu. Puisque nous cherchons, dans cette étape d’axiomatisation, des propriétés communes aux trois géométries, on peut chercher des propriétés génériques sur le cas euclidien.
Vers le premier axiome de tri-réflexions.
Dans la figure suivante, trois droites, que l’on nommera \(a, \, b \, c\) sont pilotées chacune par deux poignées, les points \(a\) et \(p_a\) pour la première (on a choisi de garder pour une poignée le nom de la droite), puis \(b\) et \(p_b\) pour la seconde et \(c\) et \(p_c\) pour la troisième. On peut manipuler chacun de ces six points dans la figure. On se donne ensuite un point \(M\) et on construit \(s_a(M)\) que l’on nomme, comme Bachmann \(M^a\), puis \(s_b \; o \; s_a(M)\), nommé \(M^{ab}\) – on rappelle que la notation la composition est inversée – et enfin \(M’= s_c \; o \; s_b \; o \; s_a(M)\) – nommé \(M^{abc}\). On construit ensuite le milieu \(I\) de \([M \, M^{abc}]\) et ensuite la perpendiculaire à ce segment en \(I\), droite rouge.
Dans le cas général, en déplaçant \(M\), la droite rouge n’est pas stable car la composée des trois symétries orthogonales n’est pas une symétrie orthogonale. Par contre si les trois droites \(a, \, b \, c\) sont concourantes, c’est le cas, et la droite rouge est bien entendu l’axe de la symétrie orthogonale.
Dans la figure ci-dessous, le point \(p_c\) est aimanté (à 5 pixels) par la situation qui rend les trois droites concourantes. On peut le déplacer, mais on obtient le même résultat avec le déplacement des cinq autres points de base qui définissent les droites. On sort facilement de l’aimantation en déplaçant rapidement un de ces points.
Rendre les trois droites concourantes et observer, en déplaçant \(M\), qu’alors la droite rouge reste stable.
Bien entendu, l’observation est basée… là encore, sur le mouvement, nous pourrions alors nous sentir, à nouveau, dans la première axiomatisation de Gonseth, mais pour Bachmann, ce mouvement n’est pas en prise avec les configurations, nous nous intéressons en réalité à l’action de la composée, et surtout, nous cherchons une situation où la recherche d’une action a un sens algébrique, donc une situation où justement, il n’y a pas de mouvement … et nous somme bien dans une seconde axiomatisation.
La lecture algébrique de cette situation est donc que la composée de trois symétries orthogonales d’axes sécants est une symétrie orthogonale – donc d’ordre 2 – quand un point est incident aux trois droites. Ce sera le premier axiome de tri-symétries.
Vers le second axiome de tri-réflexions
Voyons maintenant le second cas, quand les droites sont non sécantes. Nous dirons plutôt quand les droites ont une perpendiculaire commune. On sait que c’est équivalent dans le cas euclidien et que c’est bien le cas hyperbolique que l’on veut traiter. Dans le cas elliptique, il n’y a pas de problème ici, les deux cas (droites concourantes ou ayant une perpendiculaire commune) sont équivalents.
La figure est la même que la précédente, seules des aimantations différentes sont en jeu : les points \(p_b\) et \(p_c\) sont aimantés pour que les droites \((Bp_b)\) et \((Cp_c)\) aient une perpendiculaire commune à \((Ap_A)\).
Dans la configuration d’ouverture, il n’y a pas de droites parallèles. Commencer par rendre les droites [latex]a[/latex] et \(b\) parallèles.
Observer que la droite rouge n’est pas stable avec le déplacement de \(M\). Puis ensuite rendre les trois droites parallèles (en déplaçant \(p_c\).
Vérifier que, dans ce cas, la droite rouge est invariante au déplacement de \(M\) : on a bien, à nouveau, un élément d’ordre 2.
On aura compris que le second axiome de tri-réflexions rend compte de cette propriété, ce qui donne : si trois droites ont une perpendiculaire commune, leur composition est … une droite. Dans cet énoncé, comme plusieurs fois antérieurement dans cette section, pour préserver les représentations, nous avons choisi de mêler le point de vue des configurations et celui des transformations, autrement dit mêler la première et la seconde axiomatisation. Dans une approche algébrique où les droites du plan de Bachmann vont, en définitive, être des symétries orthogonales et les points des symétries centrales, quelle va être l’action d’une transformation sur un objet (un point ou une droite dans un premier temps) ? C’est ce que nous abordons maintenant.
Image d’un objet par une transformation. Notations diverses
Autrement dit comment définir l’image d’un point par une symétrie orthogonale ? Nous avions approché cette question sur un cas particulier en commentaire à la figure sur l’incidence. Voyons maintenant que cela se généralise sans difficulté. Nous utilisons l’opération canonique des groupes : la conjugaison. On sait que la conjugaison est un homomorphisme de groupe : si on adopte la notation exponentielle \(\gamma^\alpha\) pour cette transformation \(\gamma^\alpha=\alpha \, o \gamma \, o \, \alpha^{-1}\) on a les relations :
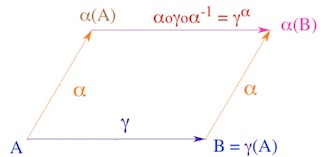
Bachmann nous fait alors observer que si on considère un groupe de bijections \(\Gamma\) sur un ensemble \(\mathcal{E}\), pour tout élément \(\gamma \in \Gamma\), et pour tout \( (A,B) \in \mathcal{E} \times \mathcal{E}\),
il y a équivalence entre :
\(\quad i) \; \gamma(A)=B\)
\(\quad ii) \;\) Pour tout \(\alpha \in \Gamma \, , \, \gamma^\alpha(\alpha(A))=\alpha(B)\)
Cela signifie que \(\gamma\), considérée comme transformation ponctuelle d’éléments de \(\mathcal{E}\), est elle-même transformée en \(\gamma^\alpha\) par toute transformation de \(\alpha \in \Gamma\). En particulier, pour ce qui est des symétries centrales et orthogonales qui nous intéressent, il vient que :
\(\quad i) \; \alpha(A)=C \; ssi \; s_{\alpha(A)}=s_A^\alpha =s_C\), et de même pour les images de droite
\(\quad ii) \; \alpha(d)=d’ \; ssi \; s_{\alpha(d)}=s_d^\alpha =s_{d’}\)
Notations utilisées par Bachmann
Ainsi, la lecture algébrique que Bachmann fait de l’image d’un point – respectivement d’une droite – par une bijection revient à la transformation d’une symétrie en la symétrie image par la conjugaison associée à la bijection.
Il est alors utile de regarder ce qu’il en est, en terme de structure, de l’ensemble \(\Delta\) des symétries orthogonales. Tout d’abord \(\Delta\) est composé d’éléments d’ordre 2, ensuite il engendre le groupe des isométries du plan, et enfin il est stable par conjugaison : \(\Delta^\alpha=\Delta\) .
À ce stade de son exposé, Bachmann pose des notations que nous allons conserver. Tout d’abord, par tradition germanique d’écriture postfixée, il note la composition \(u \; o \; v\) sous la forme \(vu\), et la conjugaison \(\gamma^\alpha=\alpha \; o \; \gamma \; o\; \alpha^{-1}\), sous forme postfixée, se note donc \(\gamma^\alpha=\alpha^{-1}\gamma\alpha\) ce qui permet d’écrire \( (\gamma^\alpha)^\beta = \gamma^{\alpha \beta}\) .
Nous avons vu que les propriétés retenues par Bachmann pour exprimer les fondements de son axiomatique sont centrées sur l’involution. Il note | la relation binaire « le produit est d’ordre 2 » : pour deux éléments \(a\) et \(b\) d’un groupe \(\mathcal{G}\), on notera désormais \(a \mid b\) pour dire que \(ab \neq 1\), l’unité du groupe et que \((ab)^2=1\).
De manière itérative il note \(a, b \mid c\) pour exprimer que \(a \mid c\) et \(b \mid c\) et de même, nous utiliserons en abrégé \(a, b \mid c, d\) pour exprimer \(a, b \mid c\) et \(a, b \mid d\).
Avec ces notations, en notant par des minuscules les symétries orthogonales identifiées à leurs axes, et des majuscules les symétries centrales identifiées à leurs centres, nous pouvons exprimer les principales propriétés de base de la géométrie euclidienne sous la forme algébrique suivante :
Les transformations sont involutives: \(a \neq 1\) et \(a^2=1\), \(P \neq 1\) et \(P ^2=1\).
L’orthogonalité : \(a \perp b\) ssi \(a \mid b\) et alors \(ab = P\).
L’incidence : \(A \, \mathfrak{I} \; d\) ssi \(A \mid d\) (et \(A \neq d\))
Remarquons que \(a \perp b\) ssi \(a^b=a\) et \(a \neq b\). De même \(A \, \mathfrak{I} \; d\) ssi \(A^d=A\) et \(A \neq d\). Cette dernière condition peut paraître inutilement insistante ; nous avons vu (menu ELL) qu’elle prendra son sens dans le contexte elliptique.
Enfin remarquons que si \(P\) est incident à \(a\) et que \(b\) soit la perpendiculaire à \(a\) en \(P\) on a les relations : \(P \mid a\) et \(a \mid b\) avec \(ab = P\) alors il vient que \(P \mid b\) et donc que \(P\) est aussi incident à \(b\) (car dans notre contexte euclidien \(P \neq b\)).