Les angles en dehors des sommets sur l’axe des ordonnés sont les angles euclidiens : le modèle est donc conforme hors de cet axe, ce qui permet d’illustrer très vite des résultats intéressants avec des figures élémentaires.
Exemples sur les triangles isocèles
Hilbert montre dans son ouvrage qu’une des conséquences de son axiome III.5 sur les liens entre les congruences des angles et des segments est ce résultats classique sur les triangles isocèles : dans un triangle \(ABC\), si les segments \([CA]\) et \([CB]\) sont congruents, alors les angles \(A\) et \(B\) du triangle \(ABC\) sont égaux.
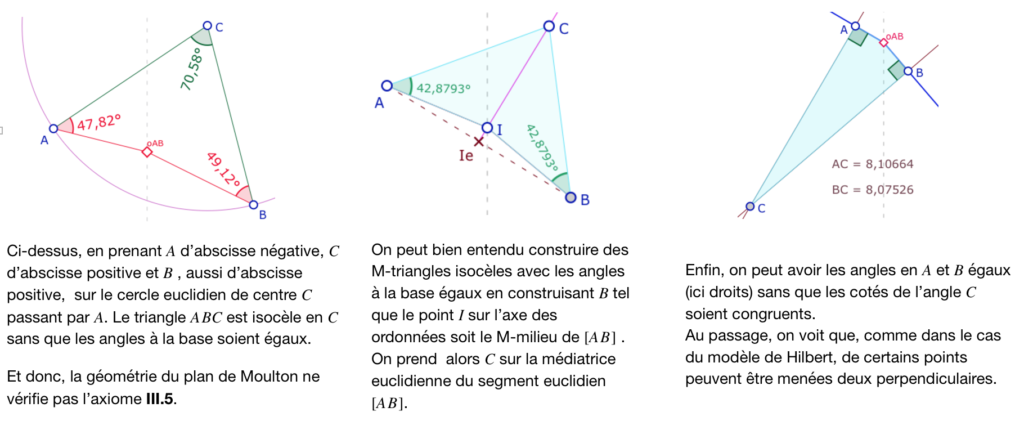
Ces premiers exemples montrent que la somme des angles d’un triangle peut être inférieure ou supérieure à deux droits.
Somme des angles d’un triangle
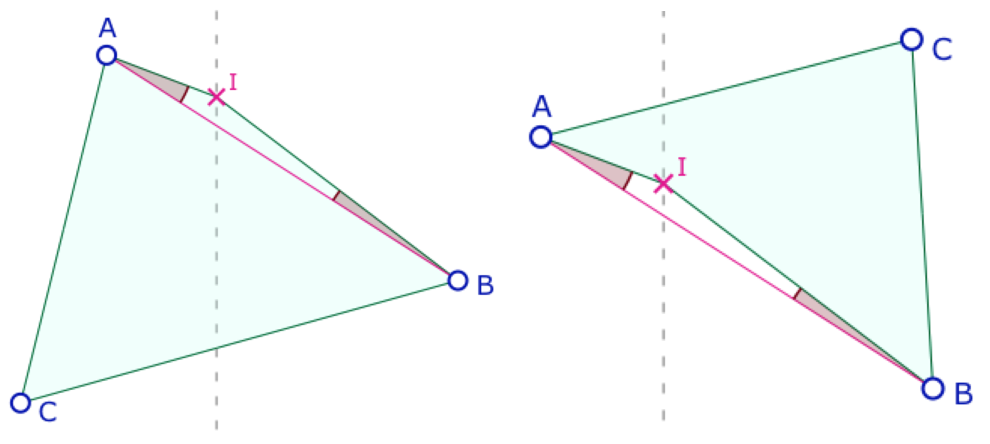
Dans un premier temps, considérons un triangle \(ABC\) dont seul le côté \([AB]\) soit un segment de Moulton non euclidien, les deux autres côtés du sommet \(C\) étant, eux, euclidiens. Alors le défaut d’angle par rapport au triangle euclidien \(ABC\) est \(\angle IAB + \angle IBA\) soit, en mesure, \(\pi – \angle AIB\) (où \(I\) est le point de rupture que l’on a nommé \(o_{AB}\) dans la page sur les droites).
On peut calculer le maximum et le minimum de ce défaut d’angle, et donc le maximum et le minimum de la somme des angles d’un triangle de Moulton. Compte tenu des pentes d’un segment de Moulton, on n’enlève rien à la généralité du calcul en considérant le schéma suivant.
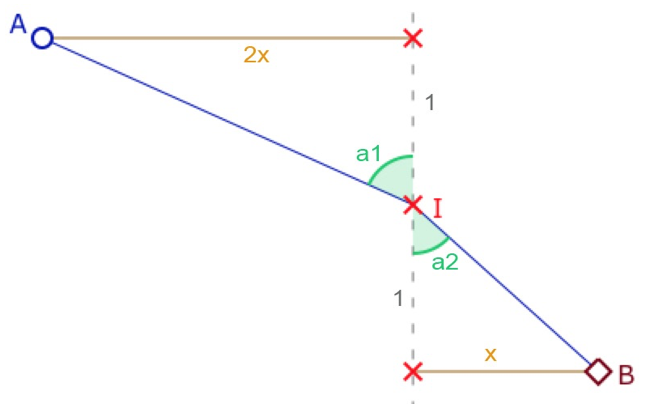
Avec les notations ci-contre, le défaut d’angle \(\pi – \angle AIB\) est alors égal à la différence d’angles \(a_1-a_2\), soit encore \(tan^{-1}(2x)-tan^{-1}(x)\).
Les formules trigonométriques d’addition permettent d’écrire \(a_1-a_2= \displaystyle tan^{-1} \left( \frac{x}{1+2x^2} \right)+k\pi\) et donc, avec la croissance de la fonction \(tan^{-1}\) on est ramené à étudier, pour \(x>0\) , le minimum de \(f(x)=\displaystyle \frac{x}{1+2x^2}\) qui est atteint en \(\displaystyle \frac{\sqrt{2}}{2}\).
Il en résulte ainsi que la somme des angles d’un triangle a pour valeurs extrêmes \(\pi \pm tan^{-1} \left( \displaystyle \frac{\sqrt{2}}{4} \right)\).
Réalisation des extrema
A partir du point de rupture du segment de Moulton placé à l’origine du repère (point \(I\)), on peut construire les points \(A\left(-\sqrt{2},1\right)\) et \(B\left(1, -\sqrt{2}\right)\) comme ci-dessous qui réalisent le défaut d’angle extrémal, maximal pour \(C\) en dessous de la droite \((AB)\) et minimal pour \(C\) en dessus.
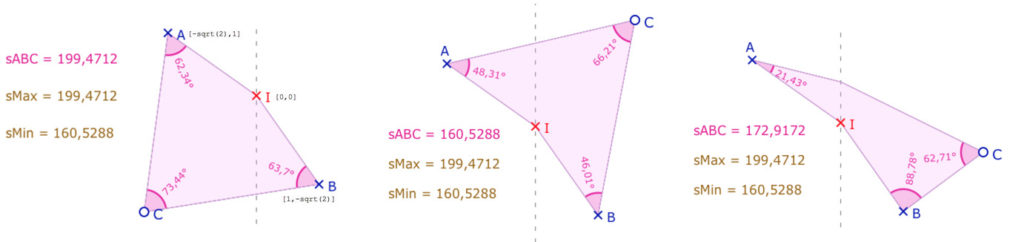
à gauche : triangle réalisant la somme des angles maximale, au centre la somme est minimale.
à droite : si le triangle a deux segments de Moulton, les valeurs extrémales ne peuvent être atteintes.
Figure d’exploration sur la somme des angles d’un triangle de Moulton
Les points \(A\) et \(B\) sont fixes, il sont sur une droite de Moulton qui permet de réaliser la somme maximale, ou minimale, pour les angles d’un triangle.
Le triangle \(PQR\) permet une exploration plus large, la droite \((PQ)\) a le même point \(I\) comme point de rupture de Moulton.
Elle doit rester à pente négative. \(P\) est un peu aimanté par la demi-droite \([AI)\) pour tester les valeurs extrémales.
On peut déplacer \(P\), en restant à abscisse négative, et \(Q\), sur la droite de Moulton \((PI)\), en restant, lui, à abscisse positive. \(R\) est déplaçable dans tout le plan.
Cas du sommet de l’angle sur l’axe des ordonnées
Moulton ayant critiqué la définition de Hilbert sur la congruence des angles dans le cas d’un point sur l’ellipse de son modèle, nous allons explorer en détail son modèle dans le seul cas où l’angle n’est pas euclidien : le cas d’un sommet sur l’axe des ordonnées … et, comme nous avons joué avec les angles sur l’ellipse dans le modèle de Hilbert (nouveau type de triangle orthocentrique), nous allons aussi jouer un peu avec les angles sur l’axe des ordonnées.
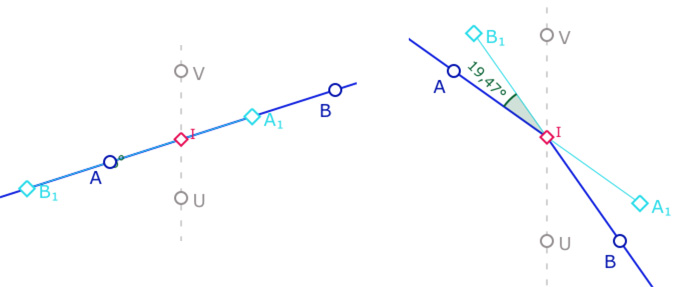
En pratique Moulton ne s’attarde pas sur le sujet, il donne une définition simple et montre qu’elle est cohérente. On rappelle que dans son article, l’axe de rupture des droites est l’axe \((OX)\) des abscisses. Moulton définit l’angle \(\angle LKM\) de sa géométrie non arguésienne comme étant l’angle euclidien \(\angle OKA_2\) ou encore, de manière plus intrinsèque, l’angle \(\angle LKP\) soit l’angle, du côté de \(M\) de la droite euclidienne \((KA_2)\). Puis il définit l’angle entre deux droites de sommet sur l’axe de rupture, comme la différence des deux angles précédemment définis. Voici l’extrait du texte original.


Nous allons reprendre cette définition dans une figure dynamique qui nous permettra d’explorer des cas particuliers intéressants. Mais tout d’abord, reprenons la définition de base, et son extension aux angles obtus, toujours avec appui sur l’axe des ordonnées \((UV)\). Rappelons que c’est le seul cas où l’angle est non conforme.
Toutefois, si la pente de la droite \((AB)\) est positive, l’angle de Moulton sur l’axe est alors l’angle euclidien, Et le défaut d’angle nul (illustration de gauche). A droite un exemple de construction de réalisation du défaut d’angle maximal.
Puis on aborde la définition plus générale, de l’angle d’un triangle dont un point est sur l’axe des ordonnées, les deux autres sommets en dehors, du même côté de l’axe, directement dans une figure dynamique
Angle en un point de l’axe – cas où les deux autres sommets sont d’un même côté de l’axe
Commencer par cacher la droite \((CD)\) par la case à cocher. Tester alors \((AB)\) à pente positive,
puis explorer la figure générale en affichant la droite \((CD)\).
Vérifier qu’on peut manuellement approcher le cas \(\angle AIC_M = \angle AIC_E\).
Réalisation de l’égalité d’angle \(\angle AIC_M = \angle AIC_E\)
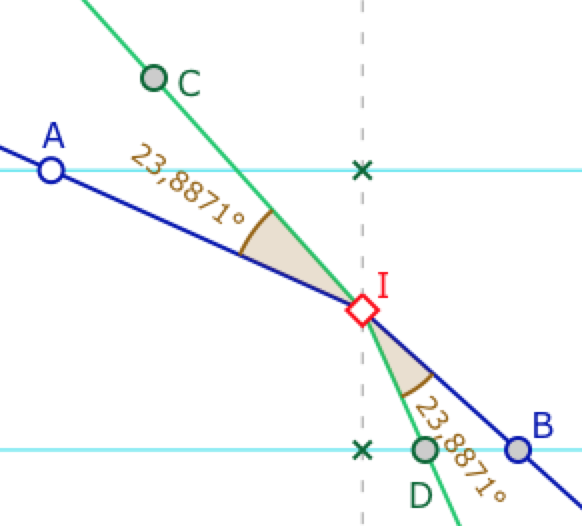
En effet, en manipulant la figure ci-dessus, on arrive à placer les points pour que un angle de Moulton en I soit (approximativement) aussi égal à son angle euclidien. On se propose désormais d’explorer ce cas si particulier.
Pour \(A\) et \(I\) donné (\(I\) d’abscisse nulle), on veut construire \(C\) tel que \(\angle AIC_M = \angle AIC_E\).
Ci-contre l’angle de Moulton \(\angle AIC_M\) est égal à\(\angle BID_E\), mais c’est aussi \(\angle AIC_E\). Dans cette figure, il n’y a que \(A\) de variable, tous les autres points sont construits. Ici, \(C\) est arbitrairement fixé sur une direction que l’on cherche à déterminer.
Pour réaliser cette figure, on reprend la démarche déjà utilisée pour les extremas de la somme des angles d’un triangle, sur la base des tangentes des angles.
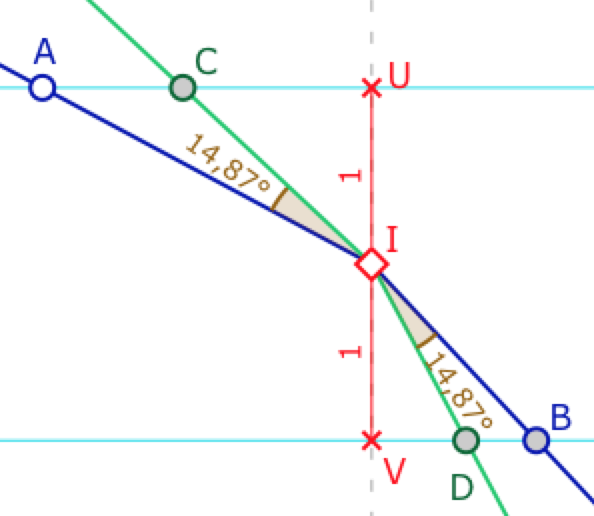
Ci-contre, \(I\) est sur l’axe des ordonnées, les segments \([IU]\) et \([IV]\) sont de mesure 1, on se donne \(A\) sur la droite horizontale passant par \(U\). C’est le seul point mobile, tous les autres sont construits. On pose \(AU=2x\), \(AC=2y\). Puisque les droites \((AB)\) et \((CD)\) sont des droites de Moulton, à pentes négatives, on a \(BV=x\) et \(BD=y\). Notons ensuite \(\alpha = \angle UIA\), \(\beta = \angle VIB\). On cherche donc à placer \(C\) pour que \(u = \angle AIC\) vérifie \(u = \angle AIC= \angle BID\).
On a donc \(tan \alpha=2x, \; tan \beta = x, \; tan(\alpha-u)=2x-2y\) et \(tan(\beta-u)=x-y\).
Partant de \(tan(\alpha-u)=2tan(\beta-u)\), avec les formules trigonométriques sur les tangentes, on trouve \(tan \, u = \left(\displaystyle \frac{2x^2-1}{3x}\right)\). On a donc directement \(u=tan^{-1} \left(\displaystyle \frac{2x^2-1}{3x}\right)\).
Solution dynamique
Dans cette figure, on ne peut que déplacer le point \(A\).
Application : construction d’un M-triangle très particulier
Fort de ce résultat, facile d’accès, nous nous proposons d’aller un peu plus loin.
Dans cette section on se propose de construire un triangle de Moulton \(AOB\) tel que
• les point \(A, O\) et \(B\) soient alignés pour la géométrie euclidienne,
• le sommet \(O\) soit un point de l’axe des ordonnées,
• la somme des angles du triangle de Moulton soit égale à deux droits.
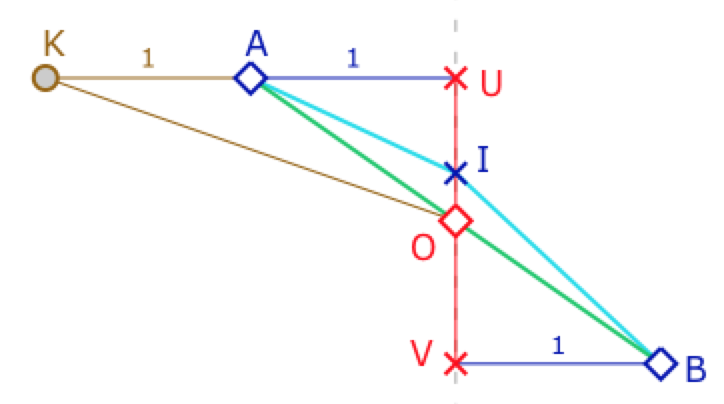
Pour simplifier les calculs, on choisit pour \(B\) le symétrique euclidien de A par rapport à \(O\). Le triangle de Moulton a trois sommets \(A, O\) et \(B\). Le point \(I\) est le point à l’origine du M-segment \([AB]\).
Pour les calculs, on utilise les triangles euclidiens \(AOI\) et \(BOI\) dans lesquels on applique Al-Kashi. Comme on va s’intéresser à la pente de la droite \((AB)\), on pose \(OU=OV=x\). \(A\) et \(B\) vérifient \(AU=BV=1\).
En appliquant la relation \(y_I = \displaystyle \frac{x_Ay_B-2x_By_A}{x_A-2x_B}\), on trouve \(y_I = \displaystyle \frac{x}{3}\). On note \(\alpha = \angle OAI\) et \(\beta = \angle OBI\).
Ce sont à la fois les angles euclidien du triangle \(ABI\) et les angles du triangle de Moulton \(AOB\). L’angle en \(O\) du triangle de Moulton \(AOB\) est le supplémentaire de \(\rho = AOK\), où \(K\) est tel que \((KB)\) soit la droite de Moulton passant par \(B\) et \(O\). Alors, résoudre ce triangle c’est chercher la direction de \((OA)\) – et donc chercher \(x\) – tel que \(\alpha+\beta=\rho\).
On part de \(AO^2=OB^2=x^2+1, \; aI^2=1+\frac{4}{9}x^2, \; IB^2= 1+\frac{16}{9}x^2, \; OI^2=\frac{x^2}{9}\) et \(OK^2=x^2+4\). Par Al-Kashi dans les triangles \(AIO\), \(IOB\) , et \(AOK\), il vient \(cos \, \alpha = \displaystyle \frac{\frac{4}{3}x^2+2}{2\sqrt{1+x^2}\sqrt{1+\frac{4}{9}x^2}}\), \(cos \, \beta = \displaystyle \frac{\left(1+\frac{15}{9} \right)x^2+2}{2\sqrt{1+x^2}\sqrt{1+\frac{16}{9}x^2}}\) et \(cos \, \rho = \displaystyle \frac{2x^2+2}{2\sqrt{1+x^2}\sqrt{x^2+4}}\).
La solution est celle de \(\rho-\alpha-\beta=0\), ce qui s’écrit aussi comme dans la figure dynamique suivante.
Triangle de Moulton particulier (sommets Euclide-alignés – somme des angles 180°)
Dans cette figure, on ne peut que déplacer le point \(A\), sur une direction donnée,et agir sur les deux cases à cocher.
Exercice: poursuivre les calculs quand \(B\) n’est pas le symétrique de \(A\) pour avoir un paramètre supplémentaire.